Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 theo chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học một cách nhanh chóng và hiệu quả nhất. Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn bộ giải đáp án đầy đủ, chính xác và dễ tiếp cận.
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh BC là số nguyên
Lời giải chi tiết:
Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
5 - 3 < BC < 5 + 3
2 < BC < 8
Mà BC là số nguyên
\(\Rightarrow BC \in\) {3;4;5;6;7} cm
Vậy độ dài BC có thể là 3 cm, 4 cm, 5 cm, 6 cm hoặc 7 cm.
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 7cm; 8cm; 11cm
b) 7cm; 9cm; 16cm
c) 8cm; 9cm; 16cm
Phương pháp giải:
So sánh độ dài cạnh lớn nhất với tổng độ dài 2 cạnh còn lại
Lời giải chi tiết:
a) Vì 7 + 8 > 11
Nên a là một tam giác theo bất đẳng thức tam giác
b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác
c) Vì 8 + 9 > 16
Nên c là một tam giác theo bất đẳng thức tam giác
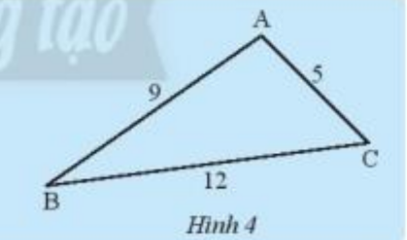
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
Phương pháp giải:
Ta so sánh tổng 2 cạnh trong tam giác với cạnh còn lại.
Lời giải chi tiết:
Trong tam giác ABC, xét tổng độ dài 2 cạnh so với cạnh còn lại :
\(\begin{array}{l}AB + AC = 9 + 5 > BC = 12\\AB + BC = 9 + 12 > AC = 5\\AC + BC = 12 + 5 > AB = 9\end{array}\)
Vậy tổng độ dài 2 cạnh trong 1 tam giác luôn lớn hơn độ dài cạnh còn lại .
Video hướng dẫn giải
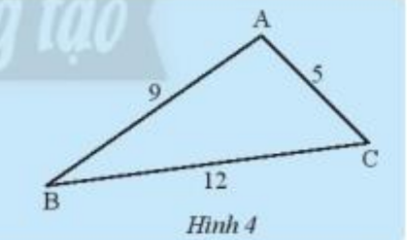
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
Phương pháp giải:
Ta so sánh tổng 2 cạnh trong tam giác với cạnh còn lại.
Lời giải chi tiết:
Trong tam giác ABC, xét tổng độ dài 2 cạnh so với cạnh còn lại :
\(\begin{array}{l}AB + AC = 9 + 5 > BC = 12\\AB + BC = 9 + 12 > AC = 5\\AC + BC = 12 + 5 > AB = 9\end{array}\)
Vậy tổng độ dài 2 cạnh trong 1 tam giác luôn lớn hơn độ dài cạnh còn lại .
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 7cm; 8cm; 11cm
b) 7cm; 9cm; 16cm
c) 8cm; 9cm; 16cm
Phương pháp giải:
So sánh độ dài cạnh lớn nhất với tổng độ dài 2 cạnh còn lại
Lời giải chi tiết:
a) Vì 7 + 8 > 11
Nên a là một tam giác theo bất đẳng thức tam giác
b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác
c) Vì 8 + 9 > 16
Nên c là một tam giác theo bất đẳng thức tam giác
Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh BC là số nguyên
Lời giải chi tiết:
Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
5 - 3 < BC < 5 + 3
2 < BC < 8
Mà BC là số nguyên
\(\Rightarrow BC \in\) {3;4;5;6;7} cm
Vậy độ dài BC có thể là 3 cm, 4 cm, 5 cm, 6 cm hoặc 7 cm.
Mục 2 của chương trình Toán 7 tập 2, Chân trời sáng tạo thường tập trung vào các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và kỹ năng trong mục này là nền tảng quan trọng cho việc học tập các kiến thức nâng cao hơn ở các lớp trên.
Để giúp các em học sinh hiểu rõ hơn về nội dung bài học và cách giải các bài tập, chúng tôi sẽ trình bày chi tiết lời giải cho từng bài tập trong mục 2 trang 45, 46 SGK Toán 7 tập 2 - Chân trời sáng tạo.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, ta cần xác định các đơn thức đồng dạng và cộng (hoặc trừ) các hệ số của chúng. Ví dụ:
3x2 + 5x - 2x2 + x = (3x2 - 2x2) + (5x + x) = x2 + 6x
Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó. Để tìm bậc của đa thức, ta cần xác định bậc của từng đơn thức trong đa thức và chọn đơn thức có bậc cao nhất. Ví dụ:
Đa thức 2x3 - 5x2 + x - 1 có bậc là 3 (vì bậc của đơn thức 2x3 là 3, và 3 lớn hơn 2, 1, và 0).
Để tính giá trị của đa thức tại một giá trị cụ thể của biến, ta thay giá trị đó vào đa thức và thực hiện các phép tính. Ví dụ:
Cho đa thức P(x) = x2 + 2x - 1. Tính P(2).
P(2) = 22 + 2*2 - 1 = 4 + 4 - 1 = 7
| Công thức | Mô tả |
|---|---|
A + B = B + A | Tính giao hoán của phép cộng |
(A + B) + C = A + (B + C) | Tính kết hợp của phép cộng |
A * B = B * A | Tính giao hoán của phép nhân |
(A * B) * C = A * (B * C) | Tính kết hợp của phép nhân |
Hy vọng rằng với lời giải chi tiết và các hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 45, 46 SGK Toán 7 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!