Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 59 và 60 sách giáo khoa Toán 7 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
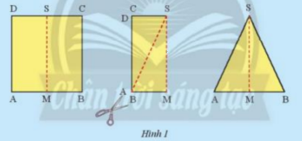
Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.
Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.
Phương pháp giải:
Gập giấy và cắt như hướng dẫn
Lời giải chi tiết:
Ta thấy sau khi cắt 2 cạnh của tam giác bằng nhau
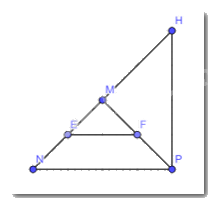
Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.
Phương pháp giải:
Dựa vào số đo các cạnh của tam giác để tìm tam giác cân
Lời giải chi tiết:
Ta thấy: \(\Delta MEF\)cân tại M do ME = MF có:
+ cạnh bên: ME, MF
+ cạnh đáy: EF
+ góc ở đỉnh: \(\widehat {EMF}\)
+ góc ở đáy: \(\widehat {MEF}\),\(\widehat {MFE}\)
\(\Delta MNP\) cân tại M do MN = MP có:
+ cạnh bên: MN, MP
+ cạnh đáy: NP
+ góc ở đỉnh: \(\widehat {NMP}\)
+ góc ở đáy: \(\widehat {NPM}\), \(\widehat {PNM}\)
\(\Delta MHP\) cân tại M do MH = MP có:
+ cạnh bên : MH, MP
+ cạnh đáy: HP
+ góc ở đỉnh: \(\widehat {PMH}\)
+ góc ở đáy: \(\widehat {MPH}\),\(\widehat {MHP}\)
Video hướng dẫn giải
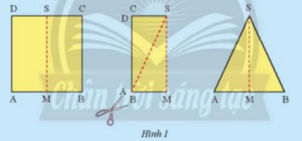
Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.
Phương pháp giải:
Gập giấy và cắt như hướng dẫn
Lời giải chi tiết:
Ta thấy sau khi cắt 2 cạnh của tam giác bằng nhau
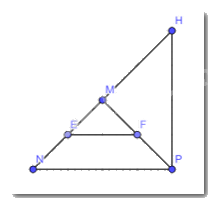
Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.
Phương pháp giải:
Dựa vào số đo các cạnh của tam giác để tìm tam giác cân
Lời giải chi tiết:
Ta thấy: \(\Delta MEF\)cân tại M do ME = MF có:
+ cạnh bên: ME, MF
+ cạnh đáy: EF
+ góc ở đỉnh: \(\widehat {EMF}\)
+ góc ở đáy: \(\widehat {MEF}\),\(\widehat {MFE}\)
\(\Delta MNP\) cân tại M do MN = MP có:
+ cạnh bên: MN, MP
+ cạnh đáy: NP
+ góc ở đỉnh: \(\widehat {NMP}\)
+ góc ở đáy: \(\widehat {NPM}\), \(\widehat {PNM}\)
\(\Delta MHP\) cân tại M do MH = MP có:
+ cạnh bên : MH, MP
+ cạnh đáy: HP
+ góc ở đỉnh: \(\widehat {PMH}\)
+ góc ở đáy: \(\widehat {MPH}\),\(\widehat {MHP}\)
Mục 1 của chương trình Toán 7 tập 2, Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Trang 59 và 60 SGK Toán 7 tập 2 Chân trời sáng tạo bao gồm các bài tập vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Các bài tập này thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ và các phép toán với số hữu tỉ.
Ví dụ:
Tính: (-1/2) + (3/4)
Lời giải:
(-1/2) + (3/4) = (-2/4) + (3/4) = 1/4
Bài 2 yêu cầu học sinh tìm giá trị của x thỏa mãn các phương trình hoặc bất phương trình chứa số hữu tỉ. Để giải bài này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình hoặc bất phương trình về dạng đơn giản và tìm ra giá trị của x.
Ví dụ:
Tìm x biết: x + (1/3) = (5/6)
Lời giải:
x = (5/6) - (1/3) = (5/6) - (2/6) = 3/6 = 1/2
Bài 3 thường là các bài toán vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần đọc kỹ đề bài, xác định các thông tin quan trọng và lựa chọn phương pháp giải phù hợp.
Ví dụ:
Một cửa hàng có 20 kg gạo. Sau khi bán đi 1/4 số gạo, cửa hàng còn lại bao nhiêu kg gạo?
Lời giải:
Số gạo đã bán là: 20 * (1/4) = 5 kg
Số gạo còn lại là: 20 - 5 = 15 kg
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 7:
Hy vọng với lời giải chi tiết và dễ hiểu cho các bài tập mục 1 trang 59, 60 SGK Toán 7 tập 2 Chân trời sáng tạo, các em học sinh sẽ tự tin hơn trong học tập và đạt kết quả tốt trong môn Toán.