Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 27 SGK Toán 7 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp học sinh dễ dàng tiếp thu và áp dụng vào các bài tập tương tự. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
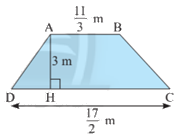
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
Đề bài
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
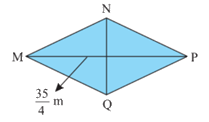
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP= \(\frac{{35}}{4}\)m. Tính độ dài NQ.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a)Diện tích hình thang =\(\dfrac{1}{2}\).(đáy lớn+đáy nhỏ).chiều cao
b)Diện tích hình thoi= \(\dfrac{1}{2}\).tích hai đường chéo
Lời giải chi tiết
a) Diện tích hình thang là:
\(\dfrac{1}{2}.\left( {AB + DC} \right).AH = \dfrac{1}{2}.\left( {\dfrac{{11}}{3} + \dfrac{{17}}{2}} \right).3 = \dfrac{{73}}{4}(m^2)\)
b) Ta có diện tích hình thoi MNPQ là \(\dfrac{{73}}{4}\,{m^2}\)
Nên ta có:
\({S_{MNPQ}} =\dfrac{{73}}{4}\\\dfrac{1}{2}.MP.NQ = \dfrac{{73}}{4}\\ \dfrac{1}{2}.\dfrac{{35}}{4}.NQ = \dfrac{{73}}{4}\\ \dfrac{{35}}{8}.NQ= \dfrac{{73}}{4} \\ NQ = \dfrac{{73}}{4}:\dfrac{{35}}{8}= \dfrac{{73}}{4}.\dfrac{{8}}{35} = \dfrac{{146}}{{35}}\)
Vậy \(NQ = \dfrac{{146}}{{35}}\) m.
Bài 6 trang 27 SGK Toán 7 tập 1 - Chân trời sáng tạo thuộc chương 1: Các số hữu tỉ, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, so sánh số hữu tỉ, hoặc tìm số hữu tỉ thỏa mãn một điều kiện nhất định.
Bài tập 6 thường bao gồm các dạng bài sau:
Để giải bài tập 6 trang 27 SGK Toán 7 tập 1 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Bài 6: Tính:
(a) −3/4 + 5/6
Giải:
Để cộng hai phân số −3/4 và 5/6, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 4 và 6 là 12.
−3/4 = −9/12
5/6 = 10/12
Vậy, −3/4 + 5/6 = −9/12 + 10/12 = 1/12
(b) 2/3 – 1/2
Giải:
Tương tự, ta quy đồng mẫu số của 2/3 và 1/2. Mẫu số chung nhỏ nhất của 3 và 2 là 6.
2/3 = 4/6
1/2 = 3/6
Vậy, 2/3 – 1/2 = 4/6 – 3/6 = 1/6
Để củng cố kiến thức về số hữu tỉ và các phép toán với số hữu tỉ, học sinh có thể tự giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài toán khó hơn.
Ngoài ra, học sinh cũng nên tìm hiểu thêm về các ứng dụng thực tế của số hữu tỉ trong đời sống, ví dụ như trong việc tính toán tiền bạc, đo lường, hoặc chia sẻ tài sản. Điều này sẽ giúp học sinh hiểu rõ hơn về tầm quan trọng của toán học trong cuộc sống.
Để học tốt môn Toán 7, học sinh cần: