Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 1 - Chân trời sáng tạo. Mục 3 trang 36 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các phép toán cơ bản và cách áp dụng vào giải quyết bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn dễ dàng tiếp thu kiến thức và tự tin giải các bài tập tương tự.
Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu. Độ dài OA có là số hữu tỉ hay không?
Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số \(\sqrt 2 \,;\frac{3}{2}\) trên trục số.
Phương pháp giải:
Trên trục số, số nhỏ hơn sẽ nằm bên trái số lớn hơn
Lời giải chi tiết:
Do \(\sqrt 2 \, = 1,41... < \frac{3}{2} = 1,5\) nên số \(\sqrt 2 \) nằm bên trái số \(\frac{3}{2}\).
Hãy biểu diễn các số thực: \( - 2;\,\, - \sqrt 2 ;\, - 1,5;\,\,2;\,3\) trên trục số.
Phương pháp giải:
Mỗi điểm trên trục số biểu diễn một số thực.
Vẽ trục số, các số thực âm nằm bên trái số 0, các số thực dương nằm bên phải số 0.
Lời giải chi tiết:

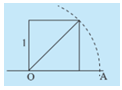
Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu. Độ dài OA có là số hữu tỉ hay không?
Phương pháp giải:
OA là đường chéo của hình vuông có cạnh là 1 => Độ dài đường chéo.
Lời giải chi tiết:
Đường chéo của hình vuông có độ dài đường chéo là 1 bằng \(\sqrt 2 \).
\(\sqrt 2 \) là số vô tỉ.
Video hướng dẫn giải
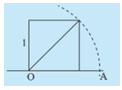
Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu. Độ dài OA có là số hữu tỉ hay không?
Phương pháp giải:
OA là đường chéo của hình vuông có cạnh là 1 => Độ dài đường chéo.
Lời giải chi tiết:
Đường chéo của hình vuông có độ dài đường chéo là 1 bằng \(\sqrt 2 \).
\(\sqrt 2 \) là số vô tỉ.
Hãy biểu diễn các số thực: \( - 2;\,\, - \sqrt 2 ;\, - 1,5;\,\,2;\,3\) trên trục số.
Phương pháp giải:
Mỗi điểm trên trục số biểu diễn một số thực.
Vẽ trục số, các số thực âm nằm bên trái số 0, các số thực dương nằm bên phải số 0.
Lời giải chi tiết:

Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số \(\sqrt 2 \,;\frac{3}{2}\) trên trục số.
Phương pháp giải:
Trên trục số, số nhỏ hơn sẽ nằm bên trái số lớn hơn
Lời giải chi tiết:
Do \(\sqrt 2 \, = 1,41... < \frac{3}{2} = 1,5\) nên số \(\sqrt 2 \) nằm bên trái số \(\frac{3}{2}\).
Mục 3 trang 36 SGK Toán 7 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về số nguyên, số hữu tỉ, và các phép toán trên chúng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc, tính chất đã học để giải quyết các bài toán thực tế.
Mục 3 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trong Mục 3 trang 36, chúng tôi sẽ trình bày chi tiết lời giải của từng bài tập:
a) 12 + (-5) = 7
b) (-8) - 3 = -11
c) 4 * (-2) = -8
d) (-15) : 3 = -5
Giải thích: Các phép tính trên được thực hiện theo quy tắc cộng, trừ, nhân, chia số nguyên đã học.
a) x + 7 = 10
x = 10 - 7
x = 3
b) x - 5 = -2
x = -2 + 5
x = 3
Giải thích: Để tìm x, ta thực hiện các phép toán ngược lại với phép toán đã cho.
Một cửa hàng có lãi 500.000 đồng trong một tuần. Hỏi trung bình mỗi ngày cửa hàng lãi bao nhiêu tiền?
Giải:
Số ngày trong một tuần là 7 ngày.
Số tiền lãi trung bình mỗi ngày là: 500.000 : 7 ≈ 71.428,57 đồng
Giải thích: Bài toán này yêu cầu học sinh áp dụng kiến thức về phép chia để tính số tiền lãi trung bình mỗi ngày.
Để học tốt môn Toán 7, bạn nên:
Mục 3 trang 36 SGK Toán 7 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này sẽ giúp bạn tự tin hơn trong các kỳ thi và học tập.
Hy vọng với hướng dẫn chi tiết và dễ hiểu trên, bạn sẽ giải quyết thành công các bài tập trong Mục 3 trang 36 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc bạn học tốt!