Chào mừng bạn đến với bài học về Lý thuyết Tập hợp các số hữu tỉ trong chương trình Toán 7 Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các số hữu tỉ, giúp bạn xây dựng nền tảng vững chắc cho các bài học tiếp theo.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, cách biểu diễn và các phép toán trên tập hợp các số hữu tỉ. Đồng thời, bài học cũng sẽ cung cấp các ví dụ minh họa và bài tập thực hành để bạn có thể áp dụng kiến thức vào giải quyết các bài toán cụ thể.
1. Số hữu tỉ
1. Số hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Tập hợp các số hữu tỉ được kí hiệu là Q
Ví dụ: \( - 7,21;\frac{{ - 7}}{{ - 9}};\frac{0}{{ - 2}};2\frac{3}{8};...\) là các số hữu tỉ
Chú ý :
+ Các số thập phân đã biết đều là các số hữu tỉ. Các số nguyên, hỗn số cũng là các số hữu tỉ
+ Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ
Ví dụ: - \(\frac{9}{{30}}\)= \(\frac{{ - 3}}{{10}}\) nên 2 phân số - \(\frac{9}{{30}}\) và \(\frac{{ - 3}}{{10}}\) cùng biểu diễn 1 số hữu tỉ
2. So sánh hai số hữu tỉ
+ Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh 2 phân số đó.
+ Với 2 số hữu tỉ a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
+ Cho 3 số hữu tỉ a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)
+ Trên trục số, nếu a < b thì điểm a nằm trước điểm b
+ Các số hữu tỉ lớn hơn 0 gọi là các số hữu tỉ dương.
+ Các số hữu tỉ nhỏ hơn 0 gọi là các số hữu tỉ âm.
+ Số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.
Chú ý: Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm; các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.
* Cách so sánh hai số hữu tỉ:
Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.
3. Biểu diễn số hữu tỉ trên trục số
Ta có thể biểu diễn mọi số hữu tỉ trên trục số
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Ta chọn phân số tối giản để biểu diễn số hữu tỉ.
4. Số đối của một số hữu tỉ
+ Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ -\(\frac{a}{b}\)
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Trên trục số, 2 điểm biểu diễn 2 số hữu tỉ đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
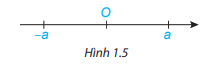
Ví dụ: -5 là số đối của 5
Trong chương trình Toán 7, việc nắm vững kiến thức về tập hợp các số hữu tỉ là vô cùng quan trọng. Đây là nền tảng để học sinh tiếp cận với các khái niệm toán học phức tạp hơn trong tương lai. Bài viết này sẽ trình bày chi tiết lý thuyết về tập hợp các số hữu tỉ theo chương trình SGK Toán 7 Chân trời sáng tạo, giúp học sinh hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Một số hữu tỉ là số có thể được viết dưới dạng phân số a/b, trong đó a là số nguyên và b là một số nguyên dương. Ví dụ: 2/3, -5/7, 0 (có thể viết là 0/1) là các số hữu tỉ.
Để biểu diễn một số hữu tỉ trên trục số, ta thực hiện các bước sau:
Có nhiều cách để so sánh các số hữu tỉ:
Các phép toán cộng, trừ, nhân, chia đều được thực hiện trên tập hợp các số hữu tỉ. Quy tắc thực hiện các phép toán này tương tự như quy tắc thực hiện các phép toán trên số nguyên.
Ví dụ:
| Phép Toán | Ví Dụ |
|---|---|
| Cộng | 1/2 + 1/3 = 5/6 |
| Trừ | 3/4 - 1/2 = 1/4 |
| Nhân | 2/5 * 3/7 = 6/35 |
| Chia | 4/9 : 2/3 = 2/3 |
Các phép toán trên tập hợp các số hữu tỉ có các tính chất sau:
Để củng cố kiến thức về tập hợp các số hữu tỉ, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết tập hợp các số hữu tỉ. Chúc bạn học tập tốt!