Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 61, 62 SGK Toán 7 tập 1 - Chân trời sáng tạo. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh cần hỗ trợ giải bài tập Toán. Chúng tôi luôn cập nhật lời giải mới nhất, chính xác nhất và trình bày một cách rõ ràng, khoa học.
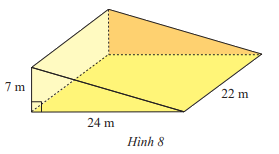
Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông.
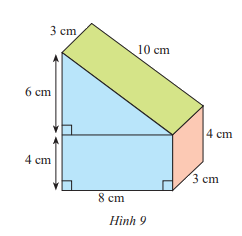
Bạn Nam đã làm một chiếc hộp hình lăng trụ đứng với kích thước như Hình 9. Bạn ấy định sơn các mặt của chiếc hộp, trừ mặt bên dưới. Tính diện tích cần sơn.
Phương pháp giải:
- Xác định đáy và các mặt bên của hình lăng trụ.
- Xác định mặt nào cần sơn
- Lập công thức tính diện tích cần sơn
Lời giải chi tiết:
Hình trên là hình lăng trụ đứng với hai đáy là hai hình thang cân có độ dài đáy nhỏ là 4cm, đáy lớn là 4 + 6 = 10cm, chiều cao là 8cm nên diện tích đáy là: Sđáy = (10+4).8 : 2 = 56 (cm2)
Hình lăng trụ đứng (đáy là hình thang cân và chiều cao là 3cm) có diện tích xung quanh là:
Sxq = Cđáy . h = (10 + 8 + 4 + 10).3 = 96 (cm2)
Vì bạn Nam định sơn tất cả các mặt trừ mặt bên dưới, mặt bên dưới là hình chữ nhật có chiều dài 8cm, chiều rộng 3cm nên diện tích mặt bên dưới là:
Shcn = 8.3 = 24 (cm2)
Diện tích phần cần sơn là:
Sxq + 2.Sđáy - Shcn = 96 + 2.56 - 24 = 184 (cm2)
Vậy diện tích cần sơn của chiếc hộp hình lăng trụ đứng là 184 cm2.
Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông.
Phương pháp giải:
Thể tích lăng trụ đứng là: V = Sđáy . h
Lời giải chi tiết:
Thể tích khối bê tông là:
V = Sđáy . h =\(\dfrac{1}{2}.24.7.22 = 1 848\) (m3)
Video hướng dẫn giải
Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông.
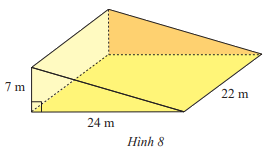
Phương pháp giải:
Thể tích lăng trụ đứng là: V = Sđáy . h
Lời giải chi tiết:
Thể tích khối bê tông là:
V = Sđáy . h =\(\dfrac{1}{2}.24.7.22 = 1 848\) (m3)
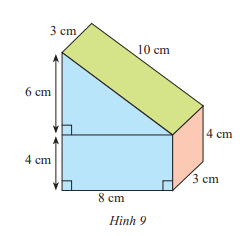
Bạn Nam đã làm một chiếc hộp hình lăng trụ đứng với kích thước như Hình 9. Bạn ấy định sơn các mặt của chiếc hộp, trừ mặt bên dưới. Tính diện tích cần sơn.
Phương pháp giải:
- Xác định đáy và các mặt bên của hình lăng trụ.
- Xác định mặt nào cần sơn
- Lập công thức tính diện tích cần sơn
Lời giải chi tiết:
Hình trên là hình lăng trụ đứng với hai đáy là hai hình thang cân có độ dài đáy nhỏ là 4cm, đáy lớn là 4 + 6 = 10cm, chiều cao là 8cm nên diện tích đáy là: Sđáy = (10+4).8 : 2 = 56 (cm2)
Hình lăng trụ đứng (đáy là hình thang cân và chiều cao là 3cm) có diện tích xung quanh là:
Sxq = Cđáy . h = (10 + 8 + 4 + 10).3 = 96 (cm2)
Vì bạn Nam định sơn tất cả các mặt trừ mặt bên dưới, mặt bên dưới là hình chữ nhật có chiều dài 8cm, chiều rộng 3cm nên diện tích mặt bên dưới là:
Shcn = 8.3 = 24 (cm2)
Diện tích phần cần sơn là:
Sxq + 2.Sđáy - Shcn = 96 + 2.56 - 24 = 184 (cm2)
Vậy diện tích cần sơn của chiếc hộp hình lăng trụ đứng là 184 cm2.
Mục 3 trong SGK Toán 7 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về số nguyên, số hữu tỉ, và các phép toán cơ bản trên chúng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, cũng như rèn luyện kỹ năng tính toán và tư duy logic.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số nguyên, đồng thời áp dụng các quy tắc về dấu của số nguyên. Ví dụ:
Lời giải cho các bài tập này đòi hỏi học sinh phải nắm vững các quy tắc về dấu của số nguyên, cũng như thực hiện các phép toán một cách chính xác.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số hữu tỉ, đồng thời áp dụng các quy tắc về dấu của số hữu tỉ. Ví dụ:
Lời giải cho các bài tập này đòi hỏi học sinh phải nắm vững các quy tắc về dấu của số hữu tỉ, cũng như thực hiện các phép toán một cách chính xác. Ngoài ra, học sinh cần chú ý đến việc quy đồng mẫu số trước khi thực hiện các phép toán cộng, trừ.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về số nguyên và số hữu tỉ để giải quyết các bài toán thực tế. Ví dụ:
Một cửa hàng bán được 150 kg gạo trong ngày đầu tiên và 120 kg gạo trong ngày thứ hai. Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu kg gạo?
Lời giải cho bài tập này đòi hỏi học sinh phải phân tích đề bài, xác định các dữ kiện cần thiết, và áp dụng các phép toán phù hợp để tìm ra kết quả.
Khi giải bài tập về số nguyên và số hữu tỉ, học sinh cần chú ý đến các quy tắc về dấu của số nguyên và số hữu tỉ. Ngoài ra, học sinh cần chú ý đến việc quy đồng mẫu số trước khi thực hiện các phép toán cộng, trừ số hữu tỉ.
Hy vọng rằng bài giải chi tiết mục 3 trang 61, 62 SGK Toán 7 tập 1 - Chân trời sáng tạo này sẽ giúp các em học sinh hiểu rõ hơn về các kiến thức về số nguyên và số hữu tỉ, đồng thời rèn luyện kỹ năng giải bài tập một cách hiệu quả. Chúc các em học tập tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Giải thích chi tiết từng bước) |
| Bài 2 | (Giải thích chi tiết từng bước) |
| Bài 3 | (Giải thích chi tiết từng bước) |