Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 1 - Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải quyết từng bước mục 2 trang 70, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn chinh phục môn Toán một cách hiệu quả.
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. ...a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
b) Vẽ \(\widehat {xOy}\) rồi vẽ \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
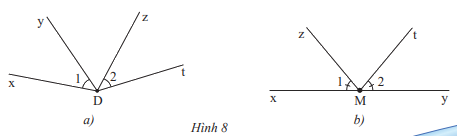
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.
Phương pháp giải:
Vẽ hình
Hai góc đối đỉnh là hai góc có chung gốc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
Lời giải chi tiết:
a)
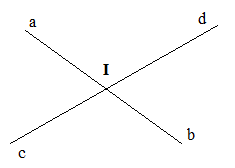
Các cặp góc đối đỉnh trên hình vẽ là: \(\widehat {aId}\) và \(\widehat {bIc}\); \(\widehat {aIc}\) và \(\widehat {bId}\)
b)
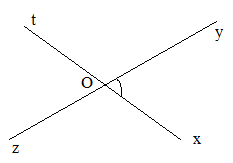
Bước 1: Vẽ góc \(\widehat {xOy}\)
Bước 2: Vẽ tia Ot là tia đối của tia Ox
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy
Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh
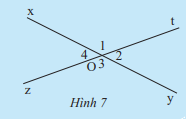
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Phương pháp giải:
Xác định các cạnh và đỉnh của các góc \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Lời giải chi tiết:
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh
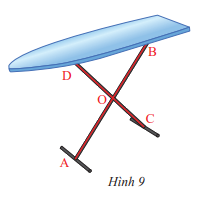
Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình
Phương pháp giải:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia
Lời giải chi tiết:
Các góc đối đỉnh trong hình là: \(\widehat {DOB}\) và \(\widehat {COA}\); \(\widehat {BOC}\) và \(\widehat {AOD}\)
Video hướng dẫn giải
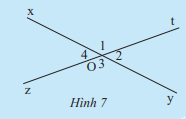
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Phương pháp giải:
Xác định các cạnh và đỉnh của các góc \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Lời giải chi tiết:
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ
b) Vẽ \(\widehat {xOy}\) rồi vẽ \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.

Phương pháp giải:
Vẽ hình
Hai góc đối đỉnh là hai góc có chung gốc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
Lời giải chi tiết:
a)
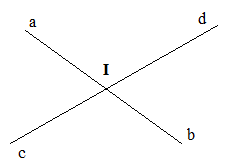
Các cặp góc đối đỉnh trên hình vẽ là: \(\widehat {aId}\) và \(\widehat {bIc}\); \(\widehat {aIc}\) và \(\widehat {bId}\)
b)
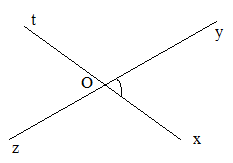
Bước 1: Vẽ góc \(\widehat {xOy}\)
Bước 2: Vẽ tia Ot là tia đối của tia Ox
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy
Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh
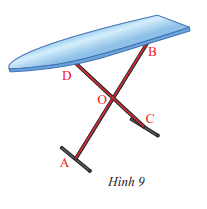
Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình
Phương pháp giải:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia
Lời giải chi tiết:
Các góc đối đỉnh trong hình là: \(\widehat {DOB}\) và \(\widehat {COA}\); \(\widehat {BOC}\) và \(\widehat {AOD}\)
Mục 2 trang 70 SGK Toán 7 tập 1 - Chân trời sáng tạo thường xoay quanh các bài tập về số nguyên, phép toán trên số nguyên, và các tính chất cơ bản của số nguyên. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 7.
Thông thường, mục 2 trang 70 sẽ bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn, chúng tôi sẽ trình bày lời giải chi tiết cho từng bài tập trong mục 2 trang 70:
Ví dụ: a) 5 + (-3) = ?
Giải:
5 + (-3) = 5 - 3 = 2
Ví dụ: x + 7 = 12
Giải:
x = 12 - 7 = 5
Ví dụ: Nhiệt độ ban ngày là 25°C, nhiệt độ ban đêm giảm 8°C. Hỏi nhiệt độ ban đêm là bao nhiêu?
Giải:
Nhiệt độ ban đêm là: 25 - 8 = 17°C
Ngoài việc giải các bài tập trong SGK, bạn có thể tìm hiểu thêm về các khái niệm liên quan đến số nguyên, như:
Để học tốt môn Toán 7, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng, với những hướng dẫn chi tiết và dễ hiểu trên đây, bạn đã có thể tự tin giải quyết các bài tập trong mục 2 trang 70 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
| Dạng bài tập | Ví dụ | Lời giải |
|---|---|---|
| Tính toán | -3 + 5 | 2 |
| Tìm x | x - 2 = 7 | x = 9 |