Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 5 trang 37 SGK Toán 7 tập 1 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 7 tập 1, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm....Tìm giá trị tuyệt đối của các số thực sau: -3,14; 41; -5; 1,(2); -5...Có bao nhiêu số thực x thoả mãn |x| = căn 3
Tìm giá trị tuyệt đối của các số thực sau: \(-3,14; 41; -5; 1,(2); -\sqrt5\).
Phương pháp giải:
|x|=x nếu x>0
|x|=-x nếu x<0
|x|=0 nếu x=0
Lời giải chi tiết:
\(\left| { - 3,14} \right| = 3,14;{\rm{ }}\,\,\,\left| {41} \right| = 41;{\rm{ }}\left| { - 5} \right| = 5;{\rm{ }}\left| {1,\left( 2 \right)} \right| = 1,(2);{\rm{ }}\left| {- \sqrt 5} \right| = \sqrt 5.\)
Có bao nhiêu số thực x thoả mãn |x| = \(\sqrt 3 \)?
Phương pháp giải:
Giá trị tuyệt đối của một số thực âm hoặc dương đều là một số hữu tỉ dương.
Lời giải chi tiết:
Có hai số thực x thỏa mãn là: \(x = \sqrt 3 ;\,\,x = - \sqrt 3 \).
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
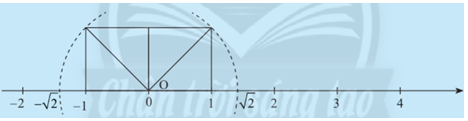
Phương pháp giải:
Quan sát hình vẽ và so sánh khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
Lời giải chi tiết:
Ta thấy khoảng cách từ 0 đến điểm \(\sqrt 2 \) bằng \(\sqrt 2 \).
Khoảng cách từ 0 đến điểm -\(\sqrt 2 \) bằng \(\sqrt 2 \)
Vậy khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \) bằng nhau.
Video hướng dẫn giải
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
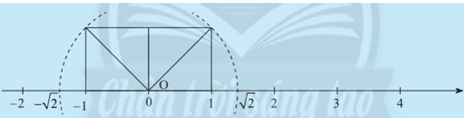
Phương pháp giải:
Quan sát hình vẽ và so sánh khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
Lời giải chi tiết:
Ta thấy khoảng cách từ 0 đến điểm \(\sqrt 2 \) bằng \(\sqrt 2 \).
Khoảng cách từ 0 đến điểm -\(\sqrt 2 \) bằng \(\sqrt 2 \)
Vậy khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \) bằng nhau.
Tìm giá trị tuyệt đối của các số thực sau: \(-3,14; 41; -5; 1,(2); -\sqrt5\).
Phương pháp giải:
|x|=x nếu x>0
|x|=-x nếu x<0
|x|=0 nếu x=0
Lời giải chi tiết:
\(\left| { - 3,14} \right| = 3,14;{\rm{ }}\,\,\,\left| {41} \right| = 41;{\rm{ }}\left| { - 5} \right| = 5;{\rm{ }}\left| {1,\left( 2 \right)} \right| = 1,(2);{\rm{ }}\left| {- \sqrt 5} \right| = \sqrt 5.\)
Có bao nhiêu số thực x thoả mãn |x| = \(\sqrt 3 \)?
Phương pháp giải:
Giá trị tuyệt đối của một số thực âm hoặc dương đều là một số hữu tỉ dương.
Lời giải chi tiết:
Có hai số thực x thỏa mãn là: \(x = \sqrt 3 ;\,\,x = - \sqrt 3 \).
Mục 5 trang 37 SGK Toán 7 tập 1 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Nội dung chính của mục này thường liên quan đến các phép toán cơ bản, các tính chất của số tự nhiên, số nguyên, và các ứng dụng của chúng trong đời sống.
Để hiểu rõ hơn về nội dung bài tập, chúng ta cần xem xét từng câu hỏi cụ thể. Thông thường, mục 5 trang 37 sẽ bao gồm các dạng bài tập sau:
Để tính giá trị của biểu thức, chúng ta cần thực hiện các phép toán theo đúng thứ tự ưu tiên: trong ngoặc trước, nhân chia trước, cộng trừ sau. Ví dụ, nếu biểu thức là 2 + 3 * 4, chúng ta sẽ thực hiện phép nhân trước (3 * 4 = 12), sau đó thực hiện phép cộng (2 + 12 = 14). Lưu ý, cần chú ý đến dấu của các số hạng và các phép toán.
Để tìm x, chúng ta cần thực hiện các phép biến đổi đại số để đưa x về một vế của phương trình. Ví dụ, nếu phương trình là 2x + 3 = 7, chúng ta sẽ trừ cả hai vế cho 3 (2x = 4), sau đó chia cả hai vế cho 2 (x = 2). Lưu ý, cần kiểm tra lại kết quả bằng cách thay x vào phương trình ban đầu.
Để giải bài toán ứng dụng, chúng ta cần đọc kỹ đề bài, xác định các yếu tố quan trọng, và lập phương trình hoặc hệ phương trình để mô tả mối quan hệ giữa các yếu tố đó. Sau đó, giải phương trình hoặc hệ phương trình để tìm ra giá trị cần tìm. Lưu ý, cần kiểm tra lại kết quả xem có phù hợp với thực tế hay không.
Để chứng minh một đẳng thức hoặc bất đẳng thức, chúng ta cần sử dụng các tính chất của số, các phép toán, và các quy tắc biến đổi đại số để đưa về một dạng tương đương. Ví dụ, để chứng minh A = B, chúng ta có thể biến đổi A thành B hoặc B thành A. Lưu ý, cần trình bày các bước chứng minh một cách rõ ràng và logic.
Khi giải bài tập mục 5 trang 37, các em cần lưu ý những điều sau:
Việc giải bài tập Toán 7 không chỉ giúp các em nắm vững kiến thức mà còn rèn luyện kỹ năng tư duy logic, khả năng giải quyết vấn đề, và sự tự tin trong học tập. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong các môn học khác và trong cuộc sống.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, và cập nhật nhanh chóng các bài tập Toán 7 tập 1 - Chân trời sáng tạo. Hãy truy cập giaitoan.edu.vn để học Toán 7 hiệu quả hơn!
Giả sử bài tập yêu cầu tính giá trị của biểu thức: (5 + 3) * 2 - 4. Chúng ta sẽ thực hiện như sau:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập mục 5 trang 37 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!