Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 65, 66 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục 3 tập trung vào các kiến thức quan trọng về...
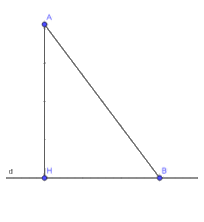
Quan sát tam giác AHB ở Hình 6. a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn b) Từ câu a, hãy giải thích vì sao AB > AH.
Quan sát tam giác AHB ở Hình 6.
a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao AB > AH.
Phương pháp giải:
- Ta sử dụng định lí về tổng số đo 3 góc trong 1 tam giác.
- Ta sử dụng định lí: Trong tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
Lời giải chi tiết:
a) Xét tam giác AHB vuông tại H ( theo giả thiết )
\( \Rightarrow \widehat {ABH} + \widehat {HAB} = {90^o}\)
\( \Rightarrow \widehat {AHB} > \widehat {ABH}\)( Do \(\widehat {AHB} = {90^o}\) và \(\widehat {ABH} < {90^o}\))
b) Xét tam giác AHB có:
\(\widehat {AHB} > \widehat {ABH}\)( chứng minh a )
Mà \(\widehat {AHB}\) đối diện với cạnh AB, \(\widehat {ABH}\) đối diện với cạnh AH.
\( \Rightarrow AB > AH\)
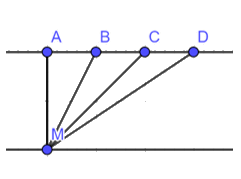
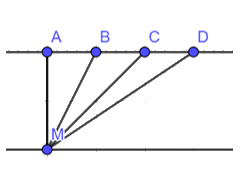
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.
Lời giải chi tiết:
Ta gọi thành hồ bơi đối diện là đường thẳng AD
Bạn Minh bơi đường ngắn nhất khi bơi từ điểm M 1 đường vuông góc với AD do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
Ta thấy AM vuông góc AD nên AM là đường ngắn nhất
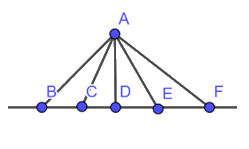
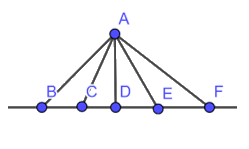
Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên
Lời giải chi tiết:
Theo hình 8 ta thấy AD là đường ngắn nhất vì AD vuông góc với BF
Các đường xiên là AB, AC, AE, AF.
Video hướng dẫn giải
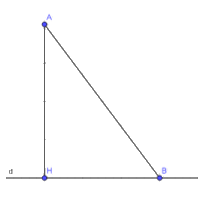
Quan sát tam giác AHB ở Hình 6.
a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao AB > AH.
Phương pháp giải:
- Ta sử dụng định lí về tổng số đo 3 góc trong 1 tam giác.
- Ta sử dụng định lí: Trong tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
Lời giải chi tiết:
a) Xét tam giác AHB vuông tại H ( theo giả thiết )
\( \Rightarrow \widehat {ABH} + \widehat {HAB} = {90^o}\)
\( \Rightarrow \widehat {AHB} > \widehat {ABH}\)( Do \(\widehat {AHB} = {90^o}\) và \(\widehat {ABH} < {90^o}\))
b) Xét tam giác AHB có:
\(\widehat {AHB} > \widehat {ABH}\)( chứng minh a )
Mà \(\widehat {AHB}\) đối diện với cạnh AB, \(\widehat {ABH}\) đối diện với cạnh AH.
\( \Rightarrow AB > AH\)
Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên
Lời giải chi tiết:
Theo hình 8 ta thấy AD là đường ngắn nhất vì AD vuông góc với BF
Các đường xiên là AB, AC, AE, AF.
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào ?
Phương pháp giải:
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.
Lời giải chi tiết:
Ta gọi thành hồ bơi đối diện là đường thẳng AD
Bạn Minh bơi đường ngắn nhất khi bơi từ điểm M 1 đường vuông góc với AD do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
Ta thấy AM vuông góc AD nên AM là đường ngắn nhất
Mục 3 trong SGK Toán 7 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về biểu thức đại số, các phép toán với biểu thức đại số, và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và phương pháp giải là vô cùng quan trọng để học tốt môn Toán.
Để thu gọn biểu thức đại số, các em cần thực hiện các bước sau:
Ví dụ: Thu gọn biểu thức 3x + 2y - x + 5y
Giải:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Để tính giá trị của biểu thức đại số, các em cần thay giá trị của các biến đã cho vào biểu thức và thực hiện các phép toán.
Ví dụ: Tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2
Giải:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Các bài toán ứng dụng thường yêu cầu các em sử dụng các kiến thức đã học để giải quyết các tình huống thực tế. Để giải các bài toán này, các em cần đọc kỹ đề bài, xác định các đại lượng cần tìm, và lập phương trình hoặc biểu thức đại số phù hợp.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng |
| a * b = b * a | Tính giao hoán của phép nhân |
| a * (b + c) = a * b + a * c | Tính chất phân phối của phép nhân đối với phép cộng |
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 65, 66 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tốt!