Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 68, 69 sách giáo khoa Toán 7 tập 2 chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án đầy đủ, chính xác và dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại.
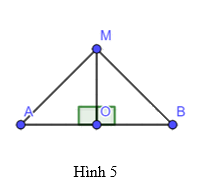
Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
Phương pháp giải:
- Chứng minh 2 tam giác bằng nhau (c-g-c)
- Từ đó suy ra các cặp cạnh tương ứng bằng nhau
Lời giải chi tiết:
Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)( do d là trung trực AB )
(c-g-c)
\( \Rightarrow MA = MB\) ( cạnh tương ứng )
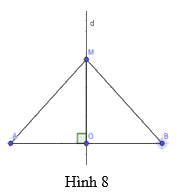
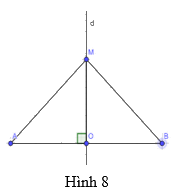
Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x
Phương pháp giải:
- Sử dụng tính chất điểm thuộc trung trực của 1 đoạn thẳng cách đều 2 đầu mút
Lời giải chi tiết:
Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5
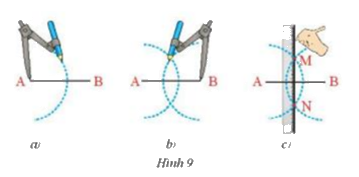
Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a)
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)
- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
Phương pháp giải:
Chứng minh M, N cùng thuộc trung trực của AB
Lời giải chi tiết:
Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn
Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn
\( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB
Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB
Video hướng dẫn giải
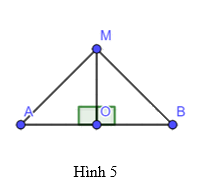
Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
Phương pháp giải:
- Chứng minh 2 tam giác bằng nhau (c-g-c)
- Từ đó suy ra các cặp cạnh tương ứng bằng nhau
Lời giải chi tiết:
Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)( do d là trung trực AB )
(c-g-c)
\( \Rightarrow MA = MB\) ( cạnh tương ứng )
Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x
Phương pháp giải:
- Sử dụng tính chất điểm thuộc trung trực của 1 đoạn thẳng cách đều 2 đầu mút
Lời giải chi tiết:
Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5
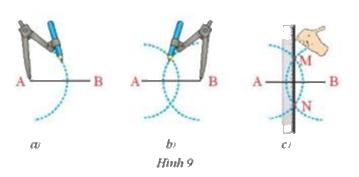
Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a)
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)
- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
Phương pháp giải:
Chứng minh M, N cùng thuộc trung trực của AB
Lời giải chi tiết:
Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn
Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn
\( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB
Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB
Mục 2 của chương trình Toán 7 tập 2 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 2 bao gồm một loạt các bài tập đa dạng, từ việc đơn giản hóa biểu thức đại số đến việc giải các phương trình đơn giản. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh áp dụng các quy tắc về phép cộng, trừ, nhân, chia đa thức để thu gọn các biểu thức đại số cho trước. Ví dụ:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Bài tập này yêu cầu học sinh thay các giá trị cụ thể của các biến vào biểu thức đại số và tính giá trị của biểu thức. Ví dụ:
Nếu x = 2 và y = -1, thì 2x + 3y = 2(2) + 3(-1) = 4 - 3 = 1
Bài tập này yêu cầu học sinh tìm giá trị của biến sao cho phương trình trở thành đúng. Ví dụ:
Để giải phương trình x + 5 = 8, ta trừ cả hai vế cho 5, ta được x = 3
Để giải các bài tập trong mục 2 một cách hiệu quả, học sinh cần:
Ví dụ 1: Thu gọn biểu thức 5x2 - 3x + 2x2 + x - 1
Giải: 5x2 - 3x + 2x2 + x - 1 = (5x2 + 2x2) + (-3x + x) - 1 = 7x2 - 2x - 1
Ví dụ 2: Tính giá trị của biểu thức 4x - 2y khi x = -1 và y = 3
Giải: 4x - 2y = 4(-1) - 2(3) = -4 - 6 = -10
Khi giải các bài tập về biểu thức đại số, cần chú ý đến thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau). Ngoài ra, cần cẩn thận với các dấu âm và dương để tránh sai sót.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 68, 69 SGK Toán 7 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!