Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 theo chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học một cách nhanh chóng và hiệu quả nhất. Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến những lời giải chính xác, đầy đủ và dễ tiếp thu.
Các bạn Bình, Mai và Lan cùng thi giải nhanh các bài toán trong sách Bài tập Toán 7. Trong một giờ, số bài làm được của mỗi bạn lần lượt là 4;3;5. Cô giáo thưởng cho mỗi bạn số hình dán lần lượt là 8;6;10. Hãy so sánh tỉ số giữa số hình dán được thưởng và số bài toán làm được của mỗi bạn
Các bạn Bình, Mai và Lan cùng thi giải nhanh các bài toán trong sách Bài tập Toán 7. Trong một giờ, số bài làm được của mỗi bạn lần lượt là 4;3;5. Cô giáo thưởng cho mỗi bạn số hình dán lần lượt là 8;6;10. Hãy so sánh tỉ số giữa số hình dán được thưởng và số bài toán làm được của mỗi bạn
Phương pháp giải:
Lời giải chi tiết:
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Bình là : \(\dfrac{3}{6} = \dfrac{1}{2}\)
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Mai là : \(\dfrac{3}{6} = \dfrac{1}{2}\)
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Lan là : \(\dfrac{5}{{10}} = \dfrac{1}{2}\)
Sau khi rút gọn ta thấy tỉ số giữa số bài làm được và hình dán được thưởng của mỗi bạn đều bằng nhau và cùng bằng \(\dfrac{1}{2}\)
Cho biết ba số a,b,c tỉ lệ với các số 2;4;6. Hãy ghi dãy tỉ số bằng nhau tương ứng
Phương pháp giải:
Lời giải chi tiết:
Theo đề bài các số a, b, c tỉ lệ với các số 2, 4, 6
\( \Rightarrow \) a : b : c = 2 : 4 : 6
\( \Rightarrow \) \(\dfrac{a}{2} = \dfrac{b}{4} = \dfrac{c}{6}\) ( Áp dụng lí thuyết về dãy tỉ số bằng nhau )
Gọi m,n,p,q là số quyển vở được chia của bốn bạn Mai, Ngọc, Phú, Quang. Cho biết số điểm 10 đạt được của bốn bạn lần lượt là 12;13;14;15 và số quyển vở được chia tỉ lệ với số điểm 10. Hãy viết dãy tỉ số bằng nhau tương ứng.
Phương pháp giải:
Lời giải chi tiết:
Tỉ số giữa số quyển vở và số điểm 10 của bạn Mai là : \(\dfrac{m}{{12}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Ngọc là : \(\dfrac{n}{{13}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Phú là : \(\dfrac{p}{{14}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Quang là : \(\dfrac{q}{{15}}\)
Từ các tỉ số trên ta lập được dãy tỉ số bằng nhau : \(\dfrac{m}{{12}} = \dfrac{n}{{13}} = \dfrac{p}{{14}} = \dfrac{q}{{15}}\)
Cho tỉ lệ thức \(\dfrac{3}{7} = \dfrac{9}{{21}}\). Hãy tính các tỉ số \(\dfrac{{3 + 9}}{{7 + 21}}\) và \(\dfrac{{3 - 9}}{{7 - 21}}\) rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.
Phương pháp giải:
Lần lượt thực hiện và tối giản các phép tính
Từ kết quả thu được và so sánh chúng với các tỉ số trong tỉ lệ đã cho
Lời giải chi tiết:
Ta có tỉ thức : \(\dfrac{3}{7} = \dfrac{9}{{21}}\)
Xét \(\dfrac{{3 + 9}}{{7 + 21}}\) = \(\dfrac{{12}}{{28}}\) = \( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 4 )
Xét \(\dfrac{{3 - 9}}{{7 - 21}}\) = \(\dfrac{{ - 6}}{{ - 14}}\)\( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 2 )
Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ số trong tỉ lệ thức đã cho .
Tìm hai số x, y biết rằng:
a) x + y = 30 và \(\dfrac{x}{2}\)= \(\dfrac{y}{3}\)
b) x – y = −21 và \(\dfrac{x}{5}\)= \(\dfrac{y}{{ - 2}}\)
Phương pháp giải:
Áp dụng tính chất \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a \pm c}}{{b \pm d}}\)
Lời giải chi tiết:
a) \(x + y = 30;\dfrac{x}{2} = \dfrac{y}{3}\) áp dụng tính chất của tỉ lệ thức ra có :
\( \Rightarrow \dfrac{{x + y}}{{2 + 3}} = \dfrac{x}{2}\)
\( \Rightarrow \dfrac{{30}}{5} = \dfrac{x}{2}\)
\( \Rightarrow 30.2 = x.5\)
\( \Rightarrow 60:5 = x\\ \Rightarrow x = 12\)
\(\Rightarrow 14 + y = 30\) (thay x vừa tìm được = 12 vào x + y = 30 để tìm ra y)
\(\Rightarrow y = 18\)
Vậy x = 12 y = 18
b) Ta có : \(\dfrac{x}{5} = \dfrac{y}{{ - 2}}\)= \(\dfrac{{x - y}}{{5 + 2}}\)( áp dụng tính chất tỉ lệ thức ) (1)
Mà theo đề bài x – y = -21
Thay -21 vào (1) ta có : \(\dfrac{{ - 21}}{7} = - 3\) \( = \dfrac{x}{5}\)
\( \Rightarrow \)x = (-3).5
\( \Rightarrow \)x = -15
Thay x bằng -15 ta có -15 – y = -21
\( \Rightarrow \)y = -15 + 21
\( \Rightarrow \)y = 6
Vậy x = -15 và y = 6
Tìm ba số x, y, z, biết x + y + z = 100 và x : y : z = 2 : 3 : 5
Phương pháp giải:
Lời giải chi tiết:
Từ dãy x : y : z = 2 : 3 : 5 ta có : \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}\)
Mà theo đề bài x + y + z = 100
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}=\dfrac{{x + y + z}}{{2 + 3 + 5}} = \dfrac{{100}}{{10}} = 10\)
\( \Rightarrow \) 10 \( = \dfrac{x}{2}\)\( \Rightarrow \) x = 10.2 = 20
\( \Rightarrow \) 10 \( = \dfrac{y}{3}\) \( \Rightarrow \) y = 10.3 = 30
\( \Rightarrow \) 10 \( = \dfrac{z}{5}\) \( \Rightarrow \) z = 10.5 = 50
Hãy giải bài toán tiền lãi ở hoạt động khởi động (trang 6)
Đầu năm, các bác Xuân, Yến, Dũng góp vốn làm ăn với số tiền lần lượt là 300 triệu đồng, 400 triệu đồng và 500 triệu đồng . Tiền lãi thu được sau một năm là 240 triệu đồng . Hãy tìm số tiền lãi mỗi bác được chia, biết rằng tiền lãi được chia tỉ lệ với số tiền đã góp .
Phương pháp giải:
Lời giải chi tiết:
Tổng số vốn của 3 bác Xuân, Yến, Dũng là : 300 + 400 + 500 = 1200 triệu đồng .
Tỉ lệ vốn của bác Xuân là : \(\dfrac{{300}}{{1200}}\)\( = \dfrac{1}{4}\)
TỈ lệ góp vốn của bác Yến là : \(\dfrac{{400}}{{1200}}\)\( = \dfrac{1}{3}\)
Tỉ lệ góp vốn của bác Dũng là : \(\dfrac{{500}}{{1200}}\) \( = \dfrac{5}{{12}}\)
Từ các tỉ lệ góp vốn trên ta tính được tỉ lệ lãi của mỗi người theo số vốn là :
Bác Xuân có số lãi là : \(\dfrac{1}{4} \times 240\)= 60 ( triệu đồng )
Bác Yến có số lãi là : \(\dfrac{1}{3} \times 240\)= 80 ( triệu đồng )
Bác Dũng có số lãi là : 240 – 80 - 60 = 100 ( triệu đồng )
Video hướng dẫn giải
Các bạn Bình, Mai và Lan cùng thi giải nhanh các bài toán trong sách Bài tập Toán 7. Trong một giờ, số bài làm được của mỗi bạn lần lượt là 4;3;5. Cô giáo thưởng cho mỗi bạn số hình dán lần lượt là 8;6;10. Hãy so sánh tỉ số giữa số hình dán được thưởng và số bài toán làm được của mỗi bạn
Phương pháp giải:
Lời giải chi tiết:
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Bình là : \(\dfrac{3}{6} = \dfrac{1}{2}\)
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Mai là : \(\dfrac{3}{6} = \dfrac{1}{2}\)
Tỉ số giữa số bài làm được và số hình dán được thưởng của bạn Lan là : \(\dfrac{5}{{10}} = \dfrac{1}{2}\)
Sau khi rút gọn ta thấy tỉ số giữa số bài làm được và hình dán được thưởng của mỗi bạn đều bằng nhau và cùng bằng \(\dfrac{1}{2}\)
Cho biết ba số a,b,c tỉ lệ với các số 2;4;6. Hãy ghi dãy tỉ số bằng nhau tương ứng
Phương pháp giải:
Lời giải chi tiết:
Theo đề bài các số a, b, c tỉ lệ với các số 2, 4, 6
\( \Rightarrow \) a : b : c = 2 : 4 : 6
\( \Rightarrow \) \(\dfrac{a}{2} = \dfrac{b}{4} = \dfrac{c}{6}\) ( Áp dụng lí thuyết về dãy tỉ số bằng nhau )
Gọi m,n,p,q là số quyển vở được chia của bốn bạn Mai, Ngọc, Phú, Quang. Cho biết số điểm 10 đạt được của bốn bạn lần lượt là 12;13;14;15 và số quyển vở được chia tỉ lệ với số điểm 10. Hãy viết dãy tỉ số bằng nhau tương ứng.
Phương pháp giải:
Lời giải chi tiết:
Tỉ số giữa số quyển vở và số điểm 10 của bạn Mai là : \(\dfrac{m}{{12}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Ngọc là : \(\dfrac{n}{{13}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Phú là : \(\dfrac{p}{{14}}\)
Tỉ số giữa số quyển vở và số điểm 10 của bạn Quang là : \(\dfrac{q}{{15}}\)
Từ các tỉ số trên ta lập được dãy tỉ số bằng nhau : \(\dfrac{m}{{12}} = \dfrac{n}{{13}} = \dfrac{p}{{14}} = \dfrac{q}{{15}}\)
Cho tỉ lệ thức \(\dfrac{3}{7} = \dfrac{9}{{21}}\). Hãy tính các tỉ số \(\dfrac{{3 + 9}}{{7 + 21}}\) và \(\dfrac{{3 - 9}}{{7 - 21}}\) rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.
Phương pháp giải:
Lần lượt thực hiện và tối giản các phép tính
Từ kết quả thu được và so sánh chúng với các tỉ số trong tỉ lệ đã cho
Lời giải chi tiết:
Ta có tỉ thức : \(\dfrac{3}{7} = \dfrac{9}{{21}}\)
Xét \(\dfrac{{3 + 9}}{{7 + 21}}\) = \(\dfrac{{12}}{{28}}\) = \( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 4 )
Xét \(\dfrac{{3 - 9}}{{7 - 21}}\) = \(\dfrac{{ - 6}}{{ - 14}}\)\( = \dfrac{3}{7}\)( chia cả tử và mẫu cho 2 )
Sau khi thực hiện tính các tỉ số ta thấy các kết quả sau khi tối giản của tỉ số bằng với các tỉ số trong tỉ lệ thức đã cho .
Tìm hai số x, y biết rằng:
a) x + y = 30 và \(\dfrac{x}{2}\)= \(\dfrac{y}{3}\)
b) x – y = −21 và \(\dfrac{x}{5}\)= \(\dfrac{y}{{ - 2}}\)
Phương pháp giải:
Áp dụng tính chất \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a \pm c}}{{b \pm d}}\)
Lời giải chi tiết:
a) \(x + y = 30;\dfrac{x}{2} = \dfrac{y}{3}\) áp dụng tính chất của tỉ lệ thức ra có :
\( \Rightarrow \dfrac{{x + y}}{{2 + 3}} = \dfrac{x}{2}\)
\( \Rightarrow \dfrac{{30}}{5} = \dfrac{x}{2}\)
\( \Rightarrow 30.2 = x.5\)
\( \Rightarrow 60:5 = x\\ \Rightarrow x = 12\)
\(\Rightarrow 14 + y = 30\) (thay x vừa tìm được = 12 vào x + y = 30 để tìm ra y)
\(\Rightarrow y = 18\)
Vậy x = 12 y = 18
b) Ta có : \(\dfrac{x}{5} = \dfrac{y}{{ - 2}}\)= \(\dfrac{{x - y}}{{5 + 2}}\)( áp dụng tính chất tỉ lệ thức ) (1)
Mà theo đề bài x – y = -21
Thay -21 vào (1) ta có : \(\dfrac{{ - 21}}{7} = - 3\) \( = \dfrac{x}{5}\)
\( \Rightarrow \)x = (-3).5
\( \Rightarrow \)x = -15
Thay x bằng -15 ta có -15 – y = -21
\( \Rightarrow \)y = -15 + 21
\( \Rightarrow \)y = 6
Vậy x = -15 và y = 6
a) Nguyên liệu của món mứt dừa sau khi hoàn thành chỉ gồm dừa và đường theo tỷ lệ 2 : 1. Tính xem trong 6 kg mứt dừa có bao nhiêu ki-lô-gam dừa và bao nhiêu ki-lô-gam đường.
b) Bạn Dũng và bạn Thủy muốn làm mứt gừng theo công thức: Cứ 3 phần gừng thì cần 2 phần đường. Hai bạn mua 600g gừng. Hai bạn cần mua bao nhiêu gam đường?
c) Mẹ chỉ có 10 quyển vở, số vở chia cho hai chị em An và Bình. Tính số sách chia cho mỗi em, biết rằng số tuổi của An và Bình là 8; 12 và số sách tỉ lệ thuận với số tuổi
Phương pháp giải:
a) Theo tỉ lệ 2:1 thì trong 6kg mứt dừa sẽ có 3 phần nguyên liệu bằng nhau trong đó 2 phần là dừa còn lại là đường .
b) Từ số phần gừng và đường ta suy ra được tỉ lệ của gừng và đường . Sau đó lấy tỉ lệ nhân với số gừng đã mua để ra só đường cần mua .
c) Tính tỉ lệ quyển vở của 2 chị em và vì An nhỏ tuổi hơn nên tỉ lệ của An thấp hơn. Sau đó rút gọn tỉ lệ để tìm được số vở của mỗi người dựa vào số vở đã cho có ở đầu bài.
Lời giải chi tiết:
a) Tỉ lệ dừa và đường là : \(\dfrac{2}{1}\)
Ta có sơ đồ sau :
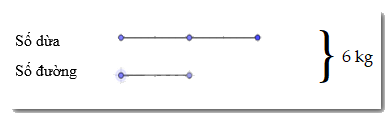
\( \Rightarrow \) Số kg đường là : 6 : ( 2+1) = 2 (kg) ( Áp dụng bài toán tổng tỉ đã học ở tiểu học )
\( \Rightarrow \) Số kg dừa là : 2 . 2 = 4 (kg)
b) Tỉ lệ của gừng và đường là 3:2 ta có được tỉ số giữa gừng và đường là \(\dfrac{3}{2}\) nên số đường bằng \(\dfrac{2}{3}\) số gừng.
Theo đề bài hai bạn đã mua 600 g gừng nên
\( \Rightarrow \) Số đường cần mua là : \(\dfrac{2}{3} \times 600\)= 400 g
Vậy 2 bạn cần mua 400g đường
c) Ta có số tuổi của An và Bình lần lượt là 8;12 nên ta sẽ có tỉ số tuổi của 2 bạn là \(\dfrac{8}{{12}} = \dfrac{2}{3}\)
Vậy số sách của An và Bình sẽ có tỉ số là 2:3
Theo đề bài chị Chi có 10 quyển vở mà theo tỉ số vừa tính được trong số 10 quyển vở đó An có 2 phần và Bình có 3 phần .
\( \Rightarrow \) Số vở của An là 10 : ( 2+3) . 2 = 4 quyển vở ( Áp dụng bài toán tổng tỉ đã được học ở lớp dưới )
\( \Rightarrow \) Số vở của Bình là : 10 – 4 = 6 quyển vở .
Tìm ba số x, y, z, biết x + y + z = 100 và x : y : z = 2 : 3 : 5
Phương pháp giải:
Lời giải chi tiết:
Từ dãy x : y : z = 2 : 3 : 5 ta có : \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}\)
Mà theo đề bài x + y + z = 100
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}=\dfrac{{x + y + z}}{{2 + 3 + 5}} = \dfrac{{100}}{{10}} = 10\)
\( \Rightarrow \) 10 \( = \dfrac{x}{2}\)\( \Rightarrow \) x = 10.2 = 20
\( \Rightarrow \) 10 \( = \dfrac{y}{3}\) \( \Rightarrow \) y = 10.3 = 30
\( \Rightarrow \) 10 \( = \dfrac{z}{5}\) \( \Rightarrow \) z = 10.5 = 50
Hãy giải bài toán tiền lãi ở hoạt động khởi động (trang 6)
Đầu năm, các bác Xuân, Yến, Dũng góp vốn làm ăn với số tiền lần lượt là 300 triệu đồng, 400 triệu đồng và 500 triệu đồng . Tiền lãi thu được sau một năm là 240 triệu đồng . Hãy tìm số tiền lãi mỗi bác được chia, biết rằng tiền lãi được chia tỉ lệ với số tiền đã góp .
Phương pháp giải:
Lời giải chi tiết:
Tổng số vốn của 3 bác Xuân, Yến, Dũng là : 300 + 400 + 500 = 1200 triệu đồng .
Tỉ lệ vốn của bác Xuân là : \(\dfrac{{300}}{{1200}}\)\( = \dfrac{1}{4}\)
TỈ lệ góp vốn của bác Yến là : \(\dfrac{{400}}{{1200}}\)\( = \dfrac{1}{3}\)
Tỉ lệ góp vốn của bác Dũng là : \(\dfrac{{500}}{{1200}}\) \( = \dfrac{5}{{12}}\)
Từ các tỉ lệ góp vốn trên ta tính được tỉ lệ lãi của mỗi người theo số vốn là :
Bác Xuân có số lãi là : \(\dfrac{1}{4} \times 240\)= 60 ( triệu đồng )
Bác Yến có số lãi là : \(\dfrac{1}{3} \times 240\)= 80 ( triệu đồng )
Bác Dũng có số lãi là : 240 – 80 - 60 = 100 ( triệu đồng )
Mục 2 trong SGK Toán 7 tập 2 chương trình Chân trời sáng tạo tập trung vào các kiến thức cơ bản về số hữu tỉ, các phép toán trên số hữu tỉ, và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Bài 1 giới thiệu khái niệm số hữu tỉ, cách biểu diễn số hữu tỉ trên trục số, và so sánh các số hữu tỉ. Các em cần hiểu rõ định nghĩa số hữu tỉ là gì, phân biệt được số hữu tỉ với số tự nhiên, số nguyên. Bài tập trong phần này thường yêu cầu các em xác định xem một số cho trước có phải là số hữu tỉ hay không, biểu diễn số hữu tỉ trên trục số, và so sánh hai số hữu tỉ.
Bài 2 hướng dẫn các em thực hiện phép cộng, trừ hai số hữu tỉ. Các em cần nắm vững quy tắc cộng, trừ hai số hữu tỉ cùng mẫu, khác mẫu, và áp dụng các quy tắc này để giải các bài tập. Bài tập trong phần này thường yêu cầu các em tính tổng, hiệu của hai số hữu tỉ, và rút gọn kết quả.
Bài 3 giới thiệu phép nhân, chia hai số hữu tỉ. Các em cần nắm vững quy tắc nhân, chia hai số hữu tỉ, và áp dụng các quy tắc này để giải các bài tập. Bài tập trong phần này thường yêu cầu các em tính tích, thương của hai số hữu tỉ, và rút gọn kết quả.
Bài 4 trình bày tính chất phân phối của phép nhân đối với phép cộng trong tập hợp số hữu tỉ. Các em cần hiểu rõ tính chất này và áp dụng nó để đơn giản hóa các biểu thức toán học. Bài tập trong phần này thường yêu cầu các em sử dụng tính chất phân phối để tính giá trị của các biểu thức.
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 2:
Các số -7; 0,5; -1/3; 2 là số hữu tỉ vì chúng có thể được viết dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0.
Để cộng hai số hữu tỉ -1/2 và 2/3, ta quy đồng mẫu số: -1/2 = -3/6 và 2/3 = 4/6. Sau đó, ta cộng hai phân số: -3/6 + 4/6 = 1/6.
Để chia hai số hữu tỉ 3/4 và -1/2, ta thực hiện phép chia: 3/4 : (-1/2) = 3/4 * (-2/1) = -6/4 = -3/2.
Hy vọng với những hướng dẫn chi tiết và hữu ích trên đây, các em sẽ tự tin hơn trong việc giải các bài tập trong mục 2 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tốt!