Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 69, 70 SGK Toán 7 tập 1 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải cụ thể, giúp các em hiểu rõ bản chất của bài toán.
a) Quan sát Hình 1 và cho biết hai góc và có:....Quan sát hình 5...Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình
Quan sát hình 5.
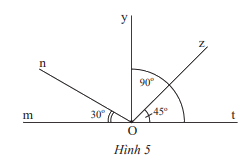
a) Tìm các góc kề với \(\widehat {tOz}\)
b) Tìm số đo của góc kề bù với \(\widehat {mOn}\).
c) Tìm số đo của \(\widehat {nOy}\)
d) Tìm số đo của góc kề bù với \(\widehat {tOz}\).
Phương pháp giải:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
Lời giải chi tiết:
a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)
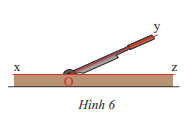
Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình
Phương pháp giải:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
2 góc vừa kề vừa bù nhau thì là hai góc kề bù
Lời giải chi tiết:
2 góc kề bù trong hình là \(\widehat {xOy}\) và \(\widehat {yOz}\)
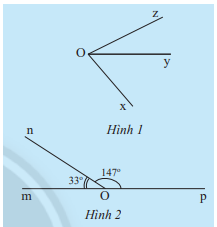
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
Phương pháp giải:
Quan sát, đo và tính
Lời giải chi tiết:
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
Video hướng dẫn giải
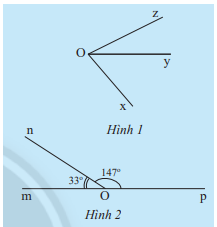
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
Phương pháp giải:
Quan sát, đo và tính
Lời giải chi tiết:
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
Quan sát hình 5.
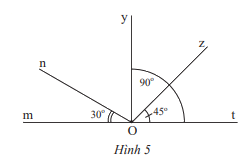
a) Tìm các góc kề với \(\widehat {tOz}\)
b) Tìm số đo của góc kề bù với \(\widehat {mOn}\).
c) Tìm số đo của \(\widehat {nOy}\)
d) Tìm số đo của góc kề bù với \(\widehat {tOz}\).
Phương pháp giải:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
Lời giải chi tiết:
a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)
Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình
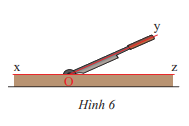
Phương pháp giải:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
2 góc vừa kề vừa bù nhau thì là hai góc kề bù
Lời giải chi tiết:
2 góc kề bù trong hình là \(\widehat {xOy}\) và \(\widehat {yOz}\)
Mục 1 trong SGK Toán 7 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức cơ bản về số tự nhiên, số nguyên, phép toán và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Bài 1 thường bao gồm các bài tập về nhận biết số tự nhiên, so sánh số tự nhiên, thực hiện các phép toán cộng, trừ, nhân, chia với số tự nhiên. Để giải tốt bài tập này, học sinh cần nắm vững các khái niệm cơ bản về số tự nhiên, các tính chất của phép cộng, trừ, nhân, chia và các quy tắc ưu tiên thực hiện các phép toán.
Bài 2 tập trung vào việc ôn tập về số nguyên, bao gồm các khái niệm về số nguyên âm, số nguyên dương, số 0, cách biểu diễn số nguyên trên trục số, so sánh số nguyên và thực hiện các phép toán cộng, trừ với số nguyên. Học sinh cần hiểu rõ khái niệm về số nguyên âm, số nguyên dương, số 0 và các quy tắc cộng, trừ số nguyên.
Bài 3 yêu cầu học sinh thực hiện các phép nhân và phép chia số nguyên, áp dụng các quy tắc về dấu trong phép nhân và phép chia. Để giải tốt bài tập này, học sinh cần nắm vững các quy tắc về dấu trong phép nhân và phép chia, và thực hành các phép toán một cách thành thạo.
Bài 4 giới thiệu về khái niệm lũy thừa với số mũ tự nhiên, các tính chất của lũy thừa và cách tính lũy thừa. Học sinh cần hiểu rõ khái niệm lũy thừa, các tính chất của lũy thừa và cách tính lũy thừa một cách chính xác.
Bài tập: Tính giá trị của biểu thức: (-3)2 + 5 - 2 x 4
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 7 tập 1 - Chân trời sáng tạo và các tài liệu tham khảo khác. Ngoài ra, các em có thể tìm kiếm các bài giảng online, video hướng dẫn giải bài tập trên giaitoan.edu.vn để học tập hiệu quả hơn.
Học Toán đòi hỏi sự kiên trì, luyện tập thường xuyên và nắm vững kiến thức cơ bản. Hãy dành thời gian ôn tập bài cũ, làm bài tập đầy đủ và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!