Chào mừng các em học sinh đến với bài học về lý thuyết Quy tắc dấu ngoặc và quy tắc chuyển vế trong chương trình Toán 7 Chân trời sáng tạo.
Đây là một trong những kiến thức nền tảng quan trọng giúp các em giải quyết các bài toán đại số một cách chính xác và hiệu quả.
Bài học này sẽ cung cấp cho các em những khái niệm cơ bản, quy tắc và ví dụ minh họa để các em có thể hiểu rõ và áp dụng vào thực tế.
1. Quy tắc dấu ngoặc
1. Quy tắc dấu ngoặc
* Khi bỏ ngoặc,
+ Nếu trước dấu ngoặc có dấu “+” thì ta bỏ ngoặc và giữ nguyên dấu của tất cả các số hạng trong ngoặc.
x + ( y + z - t) = x + y + z - t
+ Nếu trước dấu ngoặc có dấu “-” thì ta bỏ ngoặc và đổi dấu tất cả các số hạng trong ngoặc.
x – ( y + z – t) = x – y – z + t
* Đối với 1 tổng, ta có thể đổi chỗ tùy ý các số hạng, đặt dấu ngoặc để nhóm các số hạng 1 cách tùy ý.
Ví dụ:
\(\begin{array}{l}\dfrac{8}{5} - (\dfrac{5}{4} + \dfrac{3}{5} - \dfrac{1}{4})\\ = \dfrac{8}{5} - \dfrac{5}{4} - \dfrac{3}{5} + \dfrac{1}{4}\\ = \left( {\dfrac{8}{5} - \dfrac{3}{5}} \right) + \left( {\dfrac{1}{4} - \dfrac{5}{4}} \right)\\ = \dfrac{5}{5} + \dfrac{{ - 4}}{4}\\ = 1 + ( - 1)\\ = 0\end{array}\)
2. Quy tắc chuyển vế
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu của số hạng đó.
x + y = z \( \Rightarrow \) x = z – y
Ví dụ:
Tìm x, biết:
\(\dfrac{{ - 2}}{5} + x = - \dfrac{2}{3}\)
\(\begin{array}{l}x = \dfrac{{ - 2}}{3} + \dfrac{2}{5}\\x = \dfrac{{ - 10}}{{15}} + \dfrac{6}{{15}}\\x = \dfrac{{ - 4}}{{15}}\end{array}\)
Vậy \(x = \dfrac{{ - 4}}{{15}}\)
3. Thứ tự thực hiện các phép tính
* Biểu thức không có ngoặc:
+ Nếu biểu thức chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện từ trái sang phải
+ Nếu biểu thức có các phép cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện:
Lũy thừa --> Nhân, chia --> Cộng, trừ
* Biểu thức có ngoặc:
( ) --> [ ] --> { }
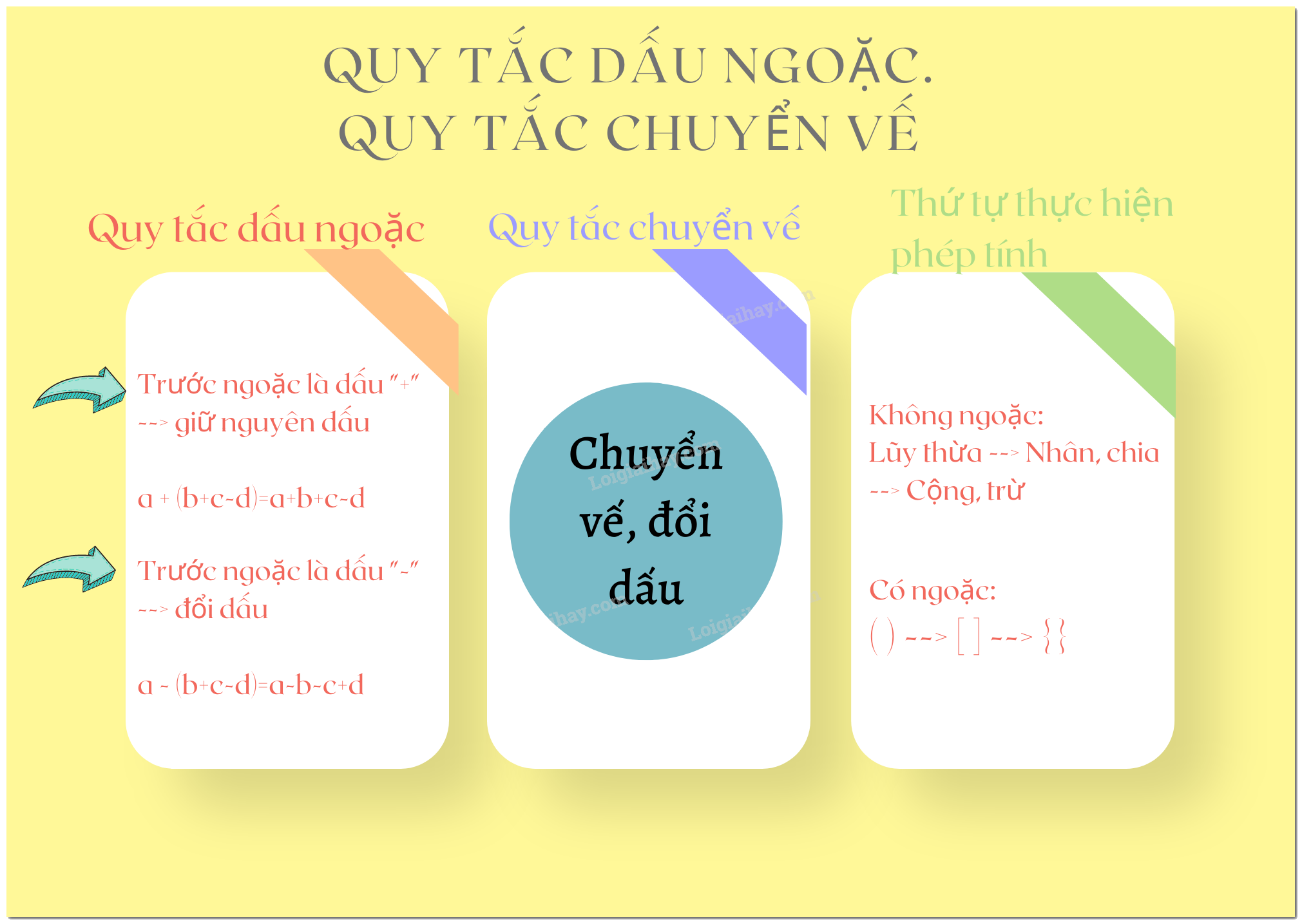
Trong chương trình Toán 7, việc nắm vững các quy tắc về dấu ngoặc và chuyển vế là vô cùng quan trọng. Đây là nền tảng để giải các phương trình và bất phương trình bậc nhất một cách chính xác. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và bài tập vận dụng để giúp các em học sinh hiểu rõ và áp dụng hiệu quả.
Quy tắc dấu ngoặc quy định cách bỏ dấu ngoặc khi trong ngoặc có các số hạng với các dấu khác nhau. Có hai trường hợp chính:
Ví dụ 1: Rút gọn biểu thức: 2x + (3x - 5)
Giải:
2x + (3x - 5) = 2x + 3x - 5 = 5x - 5
Quy tắc chuyển vế là một công cụ quan trọng để giải các phương trình. Quy tắc này cho phép ta chuyển các số hạng từ vế này sang vế kia của phương trình, đồng thời đổi dấu của chúng.
Quy tắc chuyển vế được phát biểu như sau:
Ví dụ 2: Giải phương trình: 3x + 5 = 11
Giải:
Vậy nghiệm của phương trình là x = 2.
Trong nhiều bài toán, chúng ta cần kết hợp cả hai quy tắc này để giải quyết. Hãy xem xét ví dụ sau:
Ví dụ 3: Giải phương trình: 2(x - 1) + 3 = 7
Giải:
Vậy nghiệm của phương trình là x = 3.
Để củng cố kiến thức, hãy giải các bài tập sau:
Khi áp dụng quy tắc dấu ngoặc và quy tắc chuyển vế, cần chú ý:
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết Quy tắc dấu ngoặc và quy tắc chuyển vế SGK Toán 7 Chân trời sáng tạo. Chúc các em học tập tốt!