Chào mừng bạn đến với bài học về Lý thuyết Tỉ lệ thức - Dãy tỉ số bằng nhau trong chương trình Toán 7 Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tỉ lệ thức và dãy tỉ số bằng nhau.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các ứng dụng thực tế của tỉ lệ thức, dãy tỉ số bằng nhau. Đồng thời, bài học cũng sẽ giúp bạn rèn luyện kỹ năng giải các bài tập liên quan đến chủ đề này.
Định nghĩa tỉ lệ thức
I. Các kiến thức cần nhớ
1. Tỉ lệ thức
Định nghĩa tỉ lệ thức
+ Tỉ lệ thức là đẳng thức của hai tỉ số \(\dfrac{a}{b} = \dfrac{c}{d}\)
+ Tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) còn được viết là \(a:b = c:d\)
Ví dụ: \(\dfrac{{28}}{{24}} = \dfrac{7}{6};\)\(\dfrac{3}{{10}} = \dfrac{{2,1}}{7}\)
Tính chất tỉ lệ thức
+ Tính chất 1 (tính chất cơ bản của tỉ lệ thức)
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
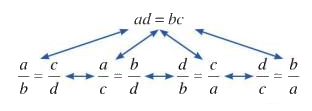
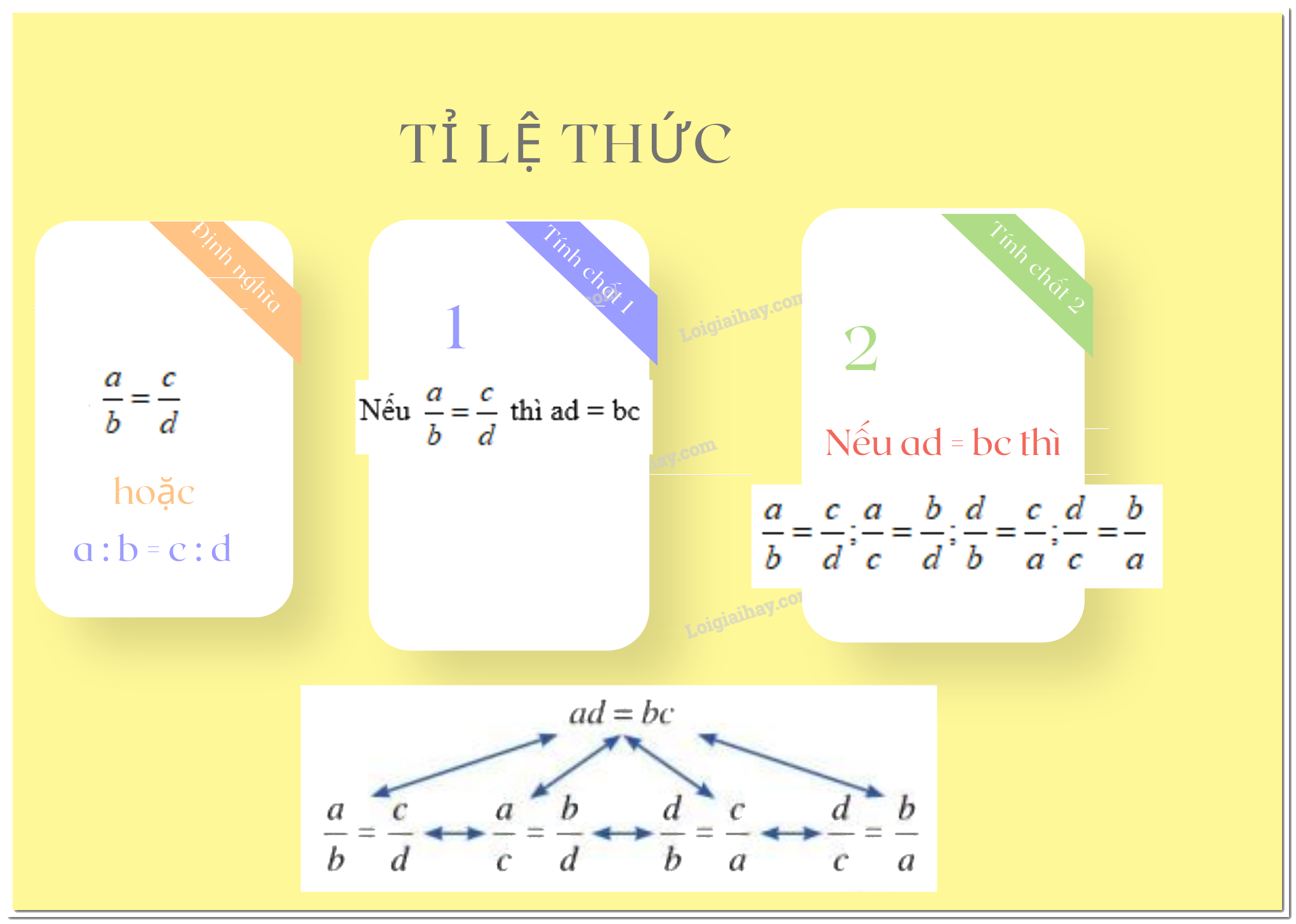
+ Tính chất 2 (điều kiện để bốn số lập thành tỉ lệ thức): Nếu \(ad=bc\) và \(a,b,c,d \ne 0\) thì ta có các tỉ lệ thức
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Ví dụ: Ta có \(\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)\)
Vì \(4.9 = 3.12(=36)\) nên ta có các tỉ lệ thức sau: \(\dfrac{4}{3} = \dfrac{{12}}{9};\,\dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}\)
2. Tính chất dãy tỉ số bằng nhau
* Ta có \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}} = \dfrac{{a - c}}{{b - d}}\)
* Từ dãy tỉ số bằng nhau \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f}\) ta suy ra:
\(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c + e}}{{b + d + f}} = \dfrac{{a - c + e}}{{b - d + f}}\)
Với điều kiện các tỉ số đều có nghĩa.
Ví dụ: \(\dfrac{{10}}{6} = \dfrac{5}{3} = \dfrac{{10 + 5}}{{6 + 3}} = \dfrac{{15}}{9}\)
\(\dfrac{{10}}{6} = \dfrac{5}{3} = \dfrac{{10 - 5}}{{6 -3}}\)
* Mở rộng
$\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{ma + nc}}{{mb + nd}} = \dfrac{{ma - nc}}{{mb - nd}}$
Ví dụ:
\(\dfrac{{10}}{6} = \dfrac{5}{3} = \dfrac{{2.10 + 3.5}}{{2.6 + 3.3}} = \dfrac{{35}}{{21}}\)
Chú ý:
Khi nói các số \(x,\,y,\,z\) tỉ lệ với các số \(a,\,b,\,c\) tức là ta có \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\). Ta cũng viết \(x:y:z = a:b:c\)
II. Các dạng toán thường gặp
Dạng 1: Lập tỉ lệ thức từ đẳng thức cho trước
Phương pháp:
Ta sử dụng: Nếu \(a.d = b.c\) thì
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Dạng 2: Tìm x, y
Phương pháp:
Sử dụng tính chất cơ bản của tỉ lệ thức: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
Trong một tỉ lệ thức ta có thể tìm một số hạng chưa biết khi biết ba số hạng còn lại.
\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a = \dfrac{{bc}}{d};\,b = \dfrac{{ad}}{c};\)\(c = \dfrac{{ad}}{b};\,d = \dfrac{{bc}}{a}\) .
Ví dụ: Tìm x biết \(\dfrac{x}{2} = \dfrac{8}{6}\)
Ta có:
\(\begin{array}{l}\dfrac{x}{2} = \dfrac{8}{6}\\\Rightarrow x.6 = 8.2\\\Rightarrow x = \dfrac{{16}}{6}\\\Rightarrow x = \dfrac{8}{3}\end{array}\)
Dạng 3: Chứng minh các tỉ lệ thức
Phương pháp:
Dựa vào các tính chất của tỉ lệ thức và biến đổi linh hoạt để chứng minh.
Dạng 4: Tìm hai số $x;y$ biết tổng (hoặc hiệu) và tỉ số của chúng.
Phương pháp giải:
* Để tìm hai số \(x;y\) khi biết tổng $x + y = s$ và tỉ số \(\dfrac{x}{y} = \dfrac{a}{b}\) ta làm như sau
Ta có \(\dfrac{x}{y} = \dfrac{a}{b} \Rightarrow \dfrac{x}{a} = \dfrac{y}{b}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x + y}}{{a + b}} = \dfrac{s}{{a + b}}\)
Từ đó \(x = \dfrac{s}{{a + b}}.a;\,y = \dfrac{s}{{a + b}}.b\) .
* Để tìm hai số \(x;y\) khi biết hiệu $x - y = p$ và tỉ số \(\dfrac{x}{y} = \dfrac{a}{b}\) ta làm như sau
Ta có \(\dfrac{x}{y} = \dfrac{a}{b}\)\( \Rightarrow \dfrac{x}{a} = \dfrac{y}{b}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{{x - y}}{{a - b}} = \dfrac{p}{{a - b}}\)
Từ đó \(x = \dfrac{p}{{a - b}}.a;\)\(y = \dfrac{p}{{a - b}}.b\) .
Ví dụ: Tìm hai số \(x;y\) biết \(\frac{x}{3} = \frac{y}{5}\) và \(x + y = - 32\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{ - 32}}{8} = - 4\)
Do đó \(\frac{x}{3} = - 4 \Rightarrow x = (-4).3 = - 12\) và \(\frac{y}{5} = - 4 \Rightarrow y = (-4).5 = - 20.\)
Vậy \(x = - 12;y = - 20.\)
Dạng 5: Chia một số thành các phần tỉ lệ với các số cho trước
Phương pháp:
Giả sử chia số \(P\) thành ba phần \(x,\,y,\,z\) tỉ lệ với các số \(a,b,c\), ta làm như sau:
\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}} = \dfrac{P}{{a + b + c}}\)
Từ đó \(x = \dfrac{P}{{a + b + c}}.a;\,y = \dfrac{P}{{a + b + c}}.b\); \(z = \dfrac{P}{{a + b + c}}.c\).
Dạng 6: Tìm hai số biết tổng và tỉ số của chúng
Phương pháp:
Tìm hai số \(x;\,y\) biết $x.y = P$ và \(\dfrac{x}{y} = \dfrac{a}{b}\)
Cách 1: Ta có \(\dfrac{x}{y} = \dfrac{a}{b} \Rightarrow \dfrac{x}{a} = \dfrac{y}{b}\)
Đặt \(\dfrac{x}{a} = \dfrac{y}{b} = k\) ta có \(x = ka;\,y = kb\)
Nên \(x.y = ka.kb = {k^2}ab = P \)\(\Rightarrow {k^2} = \dfrac{P}{{ab}}\)
Từ đó tìm được \(k\) sau đó tìm được \(x,y\).
Cách 2: Ta có \(\dfrac{x}{y} = \dfrac{a}{b}\)\( \Rightarrow \dfrac{{{x^2}}}{{xy}} = \dfrac{a}{b}\) hay \(\dfrac{{{x^2}}}{P} = \dfrac{a}{b} \)\(\Rightarrow {x^2} = \dfrac{{Pa}}{b}\) từ đó tìm được \(x\) và \(y.\)
Dạng 7: Chứng minh đẳng thức từ một tỉ lệ thức cho trước.
Phương pháp:
Áp dụng tính chất tỉ lệ thức và tính chất dãy tỉ số bằng nhau.
Dạng 8: Bài toán về tỉ lệ thức
Phương pháp:
+ Xác định mối quan hệ giữa các yếu tố của đề bài
+ Lập được tỉ lệ thức
+ Áp dụng tính chất dãy tỉ số bằng nhau để giải bài toán.
Trong chương trình Toán 7, chủ đề Tỉ lệ thức và dãy tỉ số bằng nhau đóng vai trò quan trọng trong việc xây dựng nền tảng kiến thức về đại số. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, bao gồm định nghĩa, tính chất, và các ứng dụng thực tế, đặc biệt trong bối cảnh chương trình Chân trời sáng tạo.
Tỉ lệ thức là sự bằng nhau giữa hai phân số. Nếu ta có hai phân số \frac{a}{b} và \frac{c}{d}, chúng được gọi là tỉ lệ thức nếu \frac{a}{b} = \frac{c}{d}. Trong đó, a và d là hai số hạng ngoài cùng, còn b và c là hai số hạng trong cùng.
Tính chất cơ bản của tỉ lệ thức là: Nếu \frac{a}{b} = \frac{c}{d} thì ad = bc. Đây là tính chất quan trọng để chứng minh hoặc kiểm tra tính đúng đắn của một tỉ lệ thức.
Dãy tỉ số bằng nhau là một dãy các phân số bằng nhau. Ví dụ: \frac{a}{b} = \frac{c}{d} = \frac{e}{f}. Tính chất quan trọng của dãy tỉ số bằng nhau là:
Tỉ lệ thức và dãy tỉ số bằng nhau có nhiều ứng dụng trong thực tế, bao gồm:
Ví dụ 1: Tìm x sao cho \frac{x}{3} = \frac{5}{2}.
Giải: Áp dụng tính chất của tỉ lệ thức, ta có 2x = 3 \times 5, suy ra x = \frac{15}{2}.
Ví dụ 2: Cho \frac{a}{2} = \frac{b}{3} = \frac{c}{5} và a + b + c = 20. Tìm a, b, c.
Giải: Áp dụng tính chất của dãy tỉ số bằng nhau, ta có \frac{a}{2} = \frac{b}{3} = \frac{c}{5} = \frac{a+b+c}{2+3+5} = \frac{20}{10} = 2. Suy ra a = 4, b = 6, c = 10.
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Lý thuyết Tỉ lệ thức và dãy tỉ số bằng nhau là một phần quan trọng của chương trình Toán 7. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết nhiều bài toán thực tế và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn. Hãy luyện tập thường xuyên để hiểu sâu và áp dụng thành thạo các khái niệm và tính chất đã học.