Chào mừng các em học sinh đến với lời giải chi tiết Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án đầy đủ, dễ hiểu, cùng với phương pháp giải bài tập một cách hiệu quả.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
Đề bài
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
a) Chứng minh rằng \(\Delta \)MFN = \(\Delta \)PFD
b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta \)MFN = \(\Delta \)PFD theo trường họp cạnh góc cạnh
Sử dụng tính chất của điểm đối xứng qua một điểm, trung điểm của 1 đoạn thẳng và 2 góc đối đỉnh
b) Chứng minh H là trọng tâm của tam giác MPD sau đó dựa vào tính chất ta suy ra M, H, K thẳng hàng
Lời giải chi tiết
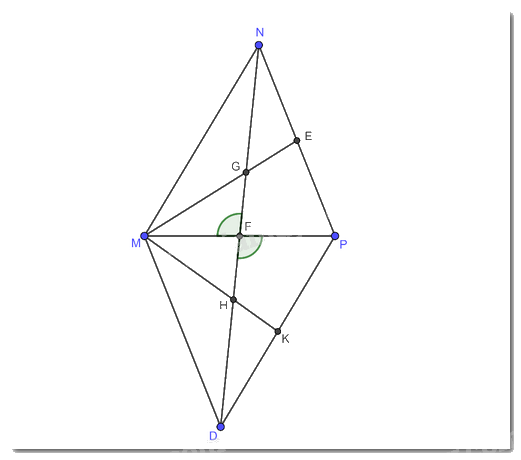
a) Vì N đối xứng với D qua F (theo giả thiết)
Nên NF = DF (1)
Vì F là trung điểm của MP (theo giả thiết)
Nên MF = PF (2)
Vì góc NFM và góc PFD ở vị trí đối đỉnh nên 2 góc bằng nhau (3)
Từ (1), (2) và (3) \( \Rightarrow \)\(\Delta \)MFN = \(\Delta \)PFD (c-g-c)
b) Xét tam giác MPD có :
F là trung điểm MD,
K là trung điểm DP (theo giả thiết)
Mà 2 đường trung tuyến của tam giác MPD là DF và MK cắt nhau tại H
\( \Rightarrow \) H là trọng tâm \(\Delta \)MPD
\( \Rightarrow \) M, H, K thẳng hàng
Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về tam giác cân, tính chất đường trung tuyến trong tam giác để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải hiểu rõ định nghĩa, tính chất của tam giác cân và biết cách áp dụng các định lý liên quan.
Bài 6 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Câu hỏi trắc nghiệm thường kiểm tra khả năng hiểu và vận dụng các định nghĩa, tính chất của tam giác cân. Để giải quyết các câu hỏi này, học sinh cần đọc kỹ đề bài, xác định đúng các yếu tố liên quan và lựa chọn đáp án phù hợp.
Phần tự luận yêu cầu học sinh trình bày lời giải chi tiết, rõ ràng, có căn cứ. Để đạt điểm cao, học sinh cần:
Bài toán: Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD là đường phân giác của góc BAC.
Lời giải:
Ngoài SGK Toán 7 tập 2 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác cân và tính chất đường trung tuyến. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên đây, các em sẽ tự tin giải quyết bài tập một cách hiệu quả. Chúc các em học tốt!