Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 theo chương trình Chân trời sáng tạo. Mục 1 trang 67 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và kỹ năng đã được học.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn hiểu sâu sắc về bài toán.
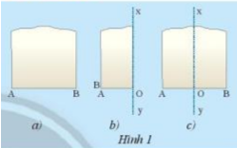
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b) Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
Phương pháp giải:
- Gấp theo hướng dẫn
Lời giải chi tiết:
Sau khi gấp A trùng với B thì điểm gấp trên cạnh AB là O
\( \Rightarrow \) AO = BO \( \Rightarrow \)O là trung điểm AB
Vì 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy .
Mà 2 cạnh của tờ giấy vuông góc với AB nên xy cũng vuông góc với AB
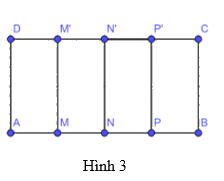
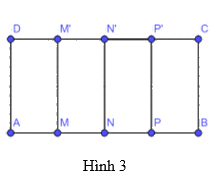
Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.
Phương pháp giải:
- Dựa vào định nghĩa của đường trung trực
Lời giải chi tiết:
Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB.
Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN.
Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB.
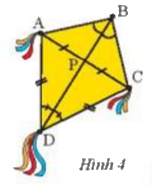
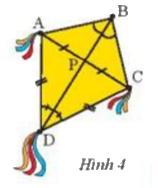
Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?
Phương pháp giải:
- Chứng minh P là trung điểm AC
- Chứng minh BD vuông góc với AC
Lời giải chi tiết:
Theo giả thiết ta có P là trung điểm AC
Xét tam giác APD và tam giác CPD có :
AP = PC ( theo giả thiết )
DP cạnh chung
AD = CD ( theo giả thiết )
Suy ra t\(\Delta APD = \Delta CPD (c-c-c)\)
\( \Rightarrow \widehat {CPD} = \widehat {APD}\) (2 góc tương ứng )
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {CPD} = \widehat {APD} = {90^o}\)\( \Rightarrow AC \bot BD\) và P là chung điểm AC do AP = PC
\( \Rightarrow \) BD là đường trung trực của AC
Video hướng dẫn giải
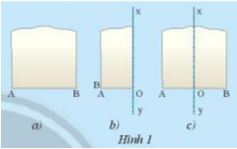
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
Phương pháp giải:
- Gấp theo hướng dẫn
Lời giải chi tiết:
Sau khi gấp A trùng với B thì điểm gấp trên cạnh AB là O
\( \Rightarrow \) AO = BO \( \Rightarrow \)O là trung điểm AB
Vì 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy .
Mà 2 cạnh của tờ giấy vuông góc với AB nên xy cũng vuông góc với AB
Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.
Phương pháp giải:
- Dựa vào định nghĩa của đường trung trực
Lời giải chi tiết:
Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB.
Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN.
Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB.
Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?
Phương pháp giải:
- Chứng minh P là trung điểm AC
- Chứng minh BD vuông góc với AC
Lời giải chi tiết:
Theo giả thiết ta có P là trung điểm AC
Xét tam giác APD và tam giác CPD có :
AP = PC ( theo giả thiết )
DP cạnh chung
AD = CD ( theo giả thiết )
Suy ra t\(\Delta APD = \Delta CPD (c-c-c)\)
\( \Rightarrow \widehat {CPD} = \widehat {APD}\) (2 góc tương ứng )
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {CPD} = \widehat {APD} = {90^o}\)\( \Rightarrow AC \bot BD\) và P là chung điểm AC do AP = PC
\( \Rightarrow \) BD là đường trung trực của AC
Mục 1 trang 67 SGK Toán 7 tập 2 - Chân trời sáng tạo thường tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc thực hiện các phép toán trên số hữu tỉ.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 67 SGK Toán 7 tập 2 - Chân trời sáng tạo:
a) \frac{2}{3} + \frac{1}{6}\
Lời giải: Để cộng hai phân số, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 3 và 6 là 6. Ta có:
\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}\
Vậy, \frac{2}{3} + \frac{1}{6} = \frac{4}{6} + \frac{1}{6} = \frac{5}{6}\
b) \frac{-5}{8} - \frac{1}{4}\
Lời giải: Tương tự như trên, ta quy đồng mẫu số. Mẫu số chung nhỏ nhất của 8 và 4 là 8. Ta có:
\frac{1}{4} = \frac{1 \times 2}{4 \times 2} = \frac{2}{8}\
Vậy, \frac{-5}{8} - \frac{1}{4} = \frac{-5}{8} - \frac{2}{8} = \frac{-7}{8}\
a) x + \frac{1}{2} = \frac{3}{4}\
Lời giải: Để tìm x, ta trừ cả hai vế của phương trình cho \frac{1}{2}\:
x = \frac{3}{4} - \frac{1}{2} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}\
b) x - \frac{2}{5} = \frac{1}{3}\
Lời giải: Để tìm x, ta cộng cả hai vế của phương trình cho \frac{2}{5}\:
x = \frac{1}{3} + \frac{2}{5} = \frac{5}{15} + \frac{6}{15} = \frac{11}{15}\
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, bạn có thể luyện tập thêm các bài tập sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày ở trên, bạn đã hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 67 SGK Toán 7 tập 2 - Chân trời sáng tạo. Chúc bạn học tập tốt!