Chào mừng các em học sinh đến với lời giải chi tiết Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án đầy đủ, dễ hiểu, cùng với phương pháp giải chi tiết để giúp các em nắm vững kiến thức và tự tin làm bài tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, mang đến những tài liệu học tập chất lượng và hữu ích nhất.
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.
Đề bài
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.
a) Chứng minh rằng AD = AC.
b) Chứng minh rằng \(\widehat {ADH} = \widehat {BAH}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Ta chứng minh tam giác ACD cân tại A sau đó suy ra AC = AD
b) Ta chứng minh \(\widehat {BAH} + \widehat {HAC} = {90^o} = \widehat {HAC} + \widehat {HCA}\) và \(\widehat D = \widehat C\)
Lời giải chi tiết
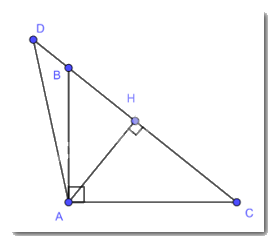
a) Xét \(\Delta AHD\) và \(\Delta AHC\) có :
AH chung
DH = HC ( C đối xứng D qua H)
\(\widehat {AHD} = \widehat {AHC} = {90^o}\)
nên \(\Delta AHD = \Delta AHC(c - g - c)\)
suy ra \(AD = AC\)(cạnh tương ứng)
Do đó \(\Delta ADC\) cân tại A suy ra \(\widehat C = \widehat D\) (góc tương ứng) (1)
b) Ta có \(\widehat {BAH} + \widehat {HAC} = {90^o}\) và \(\widehat {HCA} + \widehat {HAC} = {90^o}\)
nên \(\widehat {BAH} = \widehat {HCA}\) (2)
Từ (1) và (2) suy ra \(\widehat {ADH} = \widehat {BAH}\)
Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về tam giác cân, tính chất đường trung tuyến trong tam giác để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải có khả năng phân tích đề bài, vận dụng linh hoạt các định lý và tính chất đã học, cũng như trình bày lời giải một cách logic và rõ ràng.
Bài 3 bao gồm các câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác như:
Để giải câu a, ta cần xác định các yếu tố của tam giác cân. Dựa vào hình vẽ và thông tin đề bài, ta có thể xác định được cạnh đáy, cạnh bên, góc đáy và góc đỉnh của tam giác. Sau đó, ta vận dụng tính chất của tam giác cân để tính toán các góc và cạnh cần tìm.
Ví dụ, nếu đề bài cho biết tam giác ABC cân tại A, và góc B = 60 độ, thì ta có thể suy ra góc C = góc B = 60 độ, và góc A = 180 độ - (góc B + góc C) = 180 độ - (60 độ + 60 độ) = 60 độ. Do đó, tam giác ABC là tam giác đều.
Để giải câu b, ta cần chứng minh một đường thẳng là đường trung tuyến của tam giác. Để chứng minh một đường thẳng là đường trung tuyến của tam giác, ta cần chứng minh rằng đường thẳng đó đi qua trung điểm của một cạnh của tam giác.
Ví dụ, nếu đề bài yêu cầu chứng minh đường thẳng AM là đường trung tuyến của tam giác ABC, thì ta cần chứng minh rằng M là trung điểm của cạnh BC. Để chứng minh điều này, ta có thể sử dụng các định lý về trung điểm và đường trung tuyến trong tam giác.
Câu c thường là bài toán ứng dụng của tam giác cân trong thực tế. Để giải câu c, ta cần phân tích đề bài, vẽ hình minh họa, và vận dụng các kiến thức đã học về tam giác cân để giải quyết bài toán.
Ví dụ, nếu đề bài cho biết một chiếc thuyền có hình tam giác cân, và ta cần tính chiều cao của thuyền, thì ta có thể sử dụng các công thức tính chiều cao của tam giác cân để giải quyết bài toán.
Ngoài SGK Toán 7 tập 2 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập quan trọng, giúp các em củng cố kiến thức về tam giác cân và tính chất đường trung tuyến trong tam giác. Hy vọng rằng với lời giải chi tiết và các mẹo giải trên, các em sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.