Bài 6 trang 81 SGK Toán 7 tập 1 thuộc chương 1: Số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng kiến thức về số hữu tỉ, các phép toán trên số hữu tỉ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 81 SGK Toán 7 tập 1 - Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
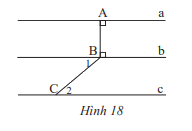
Cho Hình 18, biết (widehat {{B_1}} = 40^circ ,widehat {{C_2}} = 40^circ ) a) Đường thẳng a có song song với đường thẳng b không? Vì sao? b) Đường thẳng b có song song với đường thẳng c không? Vì sao? c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
Đề bài
Cho Hình 18, biết \(\widehat {{B_1}} = 40^\circ ,\widehat {{C_2}} = 40^\circ \)
a) Đường thẳng a có song song với đường thẳng b không? Vì sao?
b) Đường thẳng b có song song với đường thẳng c không? Vì sao?
c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
*Sử dụng dấu hiệu nhận biết 2 đường thẳng song song
*Hai đường thẳng cùng song song với 1 đường thẳng thì chúng song song
*Hai đường thẳng cùng vuông góc với 1 đường thẳng thì song song với nhau
Lời giải chi tiết
a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c
Bài 6 trang 81 SGK Toán 7 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương học về số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về số hữu tỉ, bao gồm:
Đề bài: (Đề bài cụ thể của bài 6 sẽ được trình bày đầy đủ tại đây)
Giải:
(Lời giải chi tiết, từng bước giải, kèm theo giải thích rõ ràng sẽ được trình bày tại đây. Ví dụ:)
a) Để tính giá trị của biểu thức A = (1/2) + (1/3), ta thực hiện quy đồng mẫu số:
A = (3/6) + (2/6) = (3+2)/6 = 5/6
b) Để so sánh hai số hữu tỉ x = -2/3 và y = 1/2, ta quy đồng mẫu số:
x = (-4)/6 và y = 3/6. Vì -4 < 3 nên x < y.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập về số hữu tỉ, chúng ta cùng xem xét một số ví dụ minh họa và bài tập tương tự:
Ví dụ 1: Tính giá trị của biểu thức B = (2/5) - (1/4)
Giải: B = (8/20) - (5/20) = 3/20
Bài tập 1: So sánh hai số hữu tỉ a = -1/2 và b = 3/4
Bài tập 2: Tìm x biết (x + 1/3) = 5/6
Số hữu tỉ được ứng dụng rộng rãi trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải bài tập về số hữu tỉ nói chung và bài 6 trang 81 SGK Toán 7 tập 1 - Chân trời sáng tạo nói riêng. Chúc các em học tập tốt!