Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 31, 32 SGK Toán 7 tập 1 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án đầy đủ và cách giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả và dễ dàng tiếp cận nhất cho các em.
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm. - Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN. - Tính diện tích hình vuông ABCD. - Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Hoàn thành các phát biểu sau:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số .?.
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số .?.
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số ?.
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số .?.
Phương pháp giải:
Sử dụng khái niệm số vô tỉ: Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
Lời giải chi tiết:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số hữu tỉ
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số hữu tỉ
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số vô tỉ
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số vô tỉ
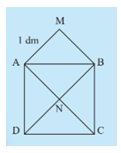
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm.
- Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN.
- Tính diện tích hình vuông ABCD.
- Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Phương pháp giải:
Diện tích hình vuông cạnh a là: a2
Lời giải chi tiết:
- Các tam giác AMB, ABN, AND, DNC, CNB có diện tích bằng nhau.
Diện tích hình vuông AMBN bằng 2 lần diện tích tam giác ANB, diện tích hình vuông ABCD bằng 4 lần diện tích tam giác ANB nên diện tích hình vuông ABCD gấp 2 lần diện tích hình vuông AMBN.
- Diện tích hình vuông ABCD là: 2.12=2 (dm2)
- Diện tích hình vuông ABCD bằng AB2
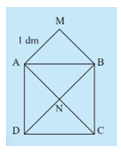
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm.
- Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN.
- Tính diện tích hình vuông ABCD.
- Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Phương pháp giải:
Diện tích hình vuông cạnh a là: a2
Lời giải chi tiết:
- Các tam giác AMB, ABN, AND, DNC, CNB có diện tích bằng nhau.
Diện tích hình vuông AMBN bằng 2 lần diện tích tam giác ANB, diện tích hình vuông ABCD bằng 4 lần diện tích tam giác ANB nên diện tích hình vuông ABCD gấp 2 lần diện tích hình vuông AMBN.
- Diện tích hình vuông ABCD là: 2.12=2 (dm2)
- Diện tích hình vuông ABCD bằng AB2
Hoàn thành các phát biểu sau:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số .?.
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số .?.
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số ?.
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số .?.
Phương pháp giải:
Sử dụng khái niệm số vô tỉ: Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
Lời giải chi tiết:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số hữu tỉ
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số hữu tỉ
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số vô tỉ
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số vô tỉ
Mục 2 trong SGK Toán 7 tập 1 - Chân trời sáng tạo tập trung vào các kiến thức cơ bản về số hữu tỉ, bao gồm các khái niệm như số hữu tỉ, số nguyên, số thập phân, phân số, và các phép toán trên số hữu tỉ. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình toán học tiếp theo.
Bài tập 1 yêu cầu các em xác định các số hữu tỉ trong một dãy số cho trước. Để giải bài tập này, các em cần nhớ lại định nghĩa của số hữu tỉ: số hữu tỉ là số có thể được biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0.
Ví dụ:
Bài tập 2 yêu cầu các em biểu diễn các số hữu tỉ sau dưới dạng phân số tối giản: 0.25, -1.5, 3/4.
Để giải bài tập này, các em cần thực hiện các bước sau:
Áp dụng các bước trên, ta có:
Bài tập 3 yêu cầu các em so sánh các số hữu tỉ: -2/3 và 1/2.
Để so sánh các số hữu tỉ, các em có thể thực hiện các bước sau:
Trong trường hợp này, ta quy đồng mẫu số của -2/3 và 1/2 thành -4/6 và 3/6. Vì -4 < 3, nên -2/3 < 1/2.
Bài tập 4 yêu cầu các em thực hiện các phép toán trên số hữu tỉ: cộng, trừ, nhân, chia.
Để thực hiện các phép toán này, các em cần nhớ lại các quy tắc sau:
Khi giải bài tập về số hữu tỉ, các em cần chú ý các điểm sau:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 31, 32 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!