Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 74, 75 SGK Toán 7 tập 2 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án đầy đủ, chính xác và dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, giaitoan.edu.vn luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học Toán một cách dễ dàng và thú vị.
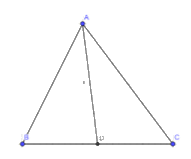
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.
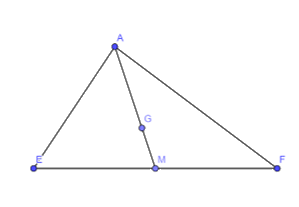
Hãy tính các tỉ số:
a) \(\dfrac{{GM}}{{AM}}\)
b) \(\dfrac{{GM}}{{AG}}\)
c) \(\dfrac{{AG}}{{GM}}\)
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy
Lời giải chi tiết:
a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :
\(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\)\( \Rightarrow \dfrac{{GM}}{{AM}} = 1 - \dfrac{2}{3} = \dfrac{1}{3}\)
b) Vì \(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\) và \(\dfrac{{GM}}{{AM}} = \dfrac{1}{3}\)(theo câu a)
\( \Rightarrow \dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)
c) Vì \(\dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)(chứng minh b)
\( \Rightarrow \dfrac{{AG}}{{GM}} = 2\)
Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy .
- Ta sẽ chứng minh AI = IJ = JD = \(\dfrac{2}{3}\)AO = \(\dfrac{2}{3}\)OD
Lời giải chi tiết:
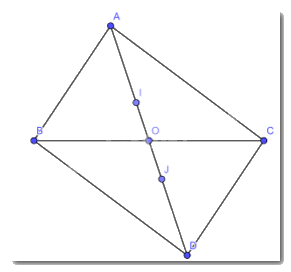
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
\(AI = \dfrac{2}{3}AO = 2IO\)(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
\(DJ = \dfrac{2}{3}OD = 2OJ\) (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
\( \Rightarrow AI = DJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD = 2OI = 2OJ\)
Mà OI = OJ do cùng \( = \dfrac{1}{3}OA = \dfrac{1}{3}OD\)(tính chất trọng tâm trong tam giác)
\( \Rightarrow 2OI = 2OJ = 2\dfrac{1}{3}AO = 2\dfrac{1}{3}OD = IJ\)
\( \Rightarrow AI = DJ = IJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD\)(điều phải chứng minh)
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số \(\dfrac{{BG}}{{BE}}\), \(\dfrac{{CG}}{{CF}}\), \(\dfrac{{AG}}{{AD}}\) bằng bao nhiêu ?
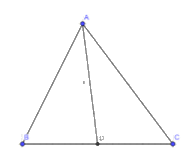
Lời giải chi tiết:
a)- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
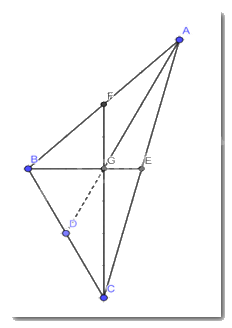
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
\(\dfrac{{BG}}{{BE}} = \dfrac{2}{3};\dfrac{{CG}}{{CF}} = \dfrac{4}{6};\dfrac{{AG}}{{AD}} = \dfrac{{4.4}}{{6.6}}\)
- Ta thấy sau khi rút gọn các tỉ số ta có :
\(\dfrac{{BG}}{{BE}} = \dfrac{{CG}}{{CF}} = \dfrac{{AG}}{{AD}} = \dfrac{2}{3}\)
Video hướng dẫn giải
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số \(\dfrac{{BG}}{{BE}}\), \(\dfrac{{CG}}{{CF}}\), \(\dfrac{{AG}}{{AD}}\) bằng bao nhiêu ?
Lời giải chi tiết:
a)- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
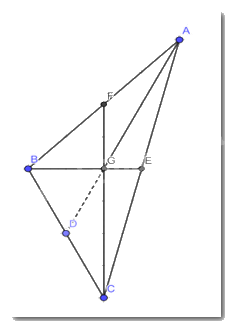
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
\(\dfrac{{BG}}{{BE}} = \dfrac{2}{3};\dfrac{{CG}}{{CF}} = \dfrac{4}{6};\dfrac{{AG}}{{AD}} = \dfrac{{4.4}}{{6.6}}\)
- Ta thấy sau khi rút gọn các tỉ số ta có :
\(\dfrac{{BG}}{{BE}} = \dfrac{{CG}}{{CF}} = \dfrac{{AG}}{{AD}} = \dfrac{2}{3}\)
Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.
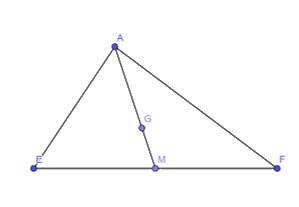
Hãy tính các tỉ số:
a) \(\dfrac{{GM}}{{AM}}\)
b) \(\dfrac{{GM}}{{AG}}\)
c) \(\dfrac{{AG}}{{GM}}\)
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy
Lời giải chi tiết:
a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :
\(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\)\( \Rightarrow \dfrac{{GM}}{{AM}} = 1 - \dfrac{2}{3} = \dfrac{1}{3}\)
b) Vì \(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\) và \(\dfrac{{GM}}{{AM}} = \dfrac{1}{3}\)(theo câu a)
\( \Rightarrow \dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)
c) Vì \(\dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)(chứng minh b)
\( \Rightarrow \dfrac{{AG}}{{GM}} = 2\)
Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy .
- Ta sẽ chứng minh AI = IJ = JD = \(\dfrac{2}{3}\)AO = \(\dfrac{2}{3}\)OD
Lời giải chi tiết:
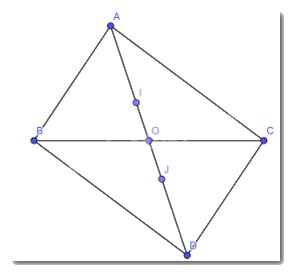
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
\(AI = \dfrac{2}{3}AO = 2IO\)(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
\(DJ = \dfrac{2}{3}OD = 2OJ\) (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
\( \Rightarrow AI = DJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD = 2OI = 2OJ\)
Mà OI = OJ do cùng \( = \dfrac{1}{3}OA = \dfrac{1}{3}OD\)(tính chất trọng tâm trong tam giác)
\( \Rightarrow 2OI = 2OJ = 2\dfrac{1}{3}AO = 2\dfrac{1}{3}OD = IJ\)
\( \Rightarrow AI = DJ = IJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD\)(điều phải chứng minh)
Mục 2 trong SGK Toán 7 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về biểu thức đại số, bao gồm các khái niệm như biến, biểu thức chứa biến, giá trị của biểu thức với một giá trị cụ thể của biến. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Để giải các bài tập trong Mục 2, các em cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, phép trừ, phép nhân, phép chia và các quy tắc về dấu ngoặc.
Bài tập này yêu cầu các em viết các biểu thức đại số biểu diễn các mối quan hệ cho trước. Ví dụ, nếu một hình chữ nhật có chiều dài là x và chiều rộng là y, thì chu vi của hình chữ nhật được biểu diễn bằng biểu thức 2(x + y).
Lời giải:
Bài tập này yêu cầu các em tính giá trị của các biểu thức đại số khi biết giá trị của các biến. Ví dụ, nếu biểu thức là 3x + 2 và x = 2, thì giá trị của biểu thức là 3(2) + 2 = 8.
Lời giải:
Bài tập này thường liên quan đến các tình huống thực tế, yêu cầu các em sử dụng kiến thức về biểu thức đại số để giải quyết. Ví dụ, một cửa hàng bán một chiếc áo với giá x đồng và giảm giá 10%, thì giá bán sau khi giảm giá là x - 0.1x = 0.9x đồng.
Lời giải: (Tương tự như các bài trên, cần phân tích đề bài và viết biểu thức đại số phù hợp để giải quyết)
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài tập trong Mục 2 trang 74, 75 SGK Toán 7 tập 2 - Chân trời sáng tạo. Chúc các em học tốt!