Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 7 tập 1, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút...Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Phương pháp giải:
Dùng máy tính cầm tay để tính các căn bậc hai số học đã cho
Lời giải chi tiết:
\(\sqrt 3 \approx 1,732...;\,\sqrt {15\,\,129} \, = 123;\,\,\,\,\,\,\sqrt {10\,\,000} = 100;\,\,\,\sqrt {10} \approx 3,162...\)
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
Phương pháp giải:
a) Độ dài cạnh bằng căn bậc hai số học của diện tích.
b) Áp dụng công thức: \(R = \sqrt {\frac{S}{\pi }} \)
Lời giải chi tiết:
a) Độ dài cạnh của một mảnh đất hình vuông là:
\(\sqrt {12\,\,996} = 114\)(m)
b) Bán kính của hình tròn là:
\(S = \pi {R^2} \Rightarrow R^2 = \frac{S}{\pi } \Rightarrow R = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{100}}{\pi }} \approx 5,64\)(cm)
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
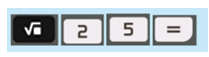
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả x trên màn hình rồi tính x2.

Phương pháp giải:
Dùng máy tính cầm tay thao tác như đề bài.
Lời giải chi tiết:
a) Kết quả trên màn hình là: 5
Suy ra: \({x^2} = {5^2} = 25\)
b) Kết quả trên màn hình là: \(1,41421...\)
Suy ra: \({x^2} = 2\)
Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Phương pháp giải:
Dùng máy tính cầm tay để tính các căn bậc hai số học đã cho
Lời giải chi tiết:
\(\sqrt 3 \approx 1,732...;\,\sqrt {15\,\,129} \, = 123;\,\,\,\,\,\,\sqrt {10\,\,000} = 100;\,\,\,\sqrt {10} \approx 3,162...\)
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
Phương pháp giải:
a) Độ dài cạnh bằng căn bậc hai số học của diện tích.
b) Áp dụng công thức: \(R = \sqrt {\frac{S}{\pi }} \)
Lời giải chi tiết:
a) Độ dài cạnh của một mảnh đất hình vuông là:
\(\sqrt {12\,\,996} = 114\)(m)
b) Bán kính của hình tròn là:
\(S = \pi {R^2} \Rightarrow R^2 = \frac{S}{\pi } \Rightarrow R = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{100}}{\pi }} \approx 5,64\)(cm)
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
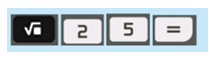
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả x trên màn hình rồi tính x2.

Phương pháp giải:
Dùng máy tính cầm tay thao tác như đề bài.
Lời giải chi tiết:
a) Kết quả trên màn hình là: 5
Suy ra: \({x^2} = {5^2} = 25\)
b) Kết quả trên màn hình là: \(1,41421...\)
Suy ra: \({x^2} = 2\)
Mục 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo thuộc chương 1: Các số hữu tỉ. Đây là một phần quan trọng trong chương trình học Toán 7, giúp học sinh làm quen với các khái niệm cơ bản về số hữu tỉ, cách biểu diễn số hữu tỉ trên trục số, và các phép toán trên số hữu tỉ.
Bài tập mục 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo bao gồm các dạng bài tập sau:
Để nhận biết một số là số hữu tỉ, ta cần kiểm tra xem số đó có thể được viết dưới dạng phân số a/b, với a và b là các số nguyên và b khác 0 hay không. Ví dụ, 2,5 là số hữu tỉ vì 2,5 = 5/2.
Để biểu diễn một số hữu tỉ trên trục số, ta thực hiện các bước sau:
Có nhiều cách để so sánh số hữu tỉ:
Để thực hiện các phép toán cộng, trừ, nhân, chia số hữu tỉ, ta thực hiện các bước sau:
Ví dụ 1: So sánh hai số hữu tỉ -1/2 và 2/3.
Ta quy đồng mẫu số của hai phân số: -1/2 = -3/6 và 2/3 = 4/6. Vì -3 < 4 nên -1/2 < 2/3.
Ví dụ 2: Tính tổng hai số hữu tỉ 1/4 và 3/5.
Ta quy đồng mẫu số của hai phân số: 1/4 = 5/20 và 3/5 = 12/20. Vậy 1/4 + 3/5 = 5/20 + 12/20 = 17/20.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải các bài tập mục 4 trang 33 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!