Chào mừng bạn đến với bài học lý thuyết về các phép toán với số hữu tỉ, một phần quan trọng trong chương trình Toán 7 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và các quy tắc cần thiết để thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng dễ hiểu, bài tập đa dạng và phương pháp học tập hiệu quả nhất.
1. Cộng và trừ hai số hữu tỉ
1. Cộng và trừ hai số hữu tỉ
a) Cộng, trừ hai số hữu tỉ
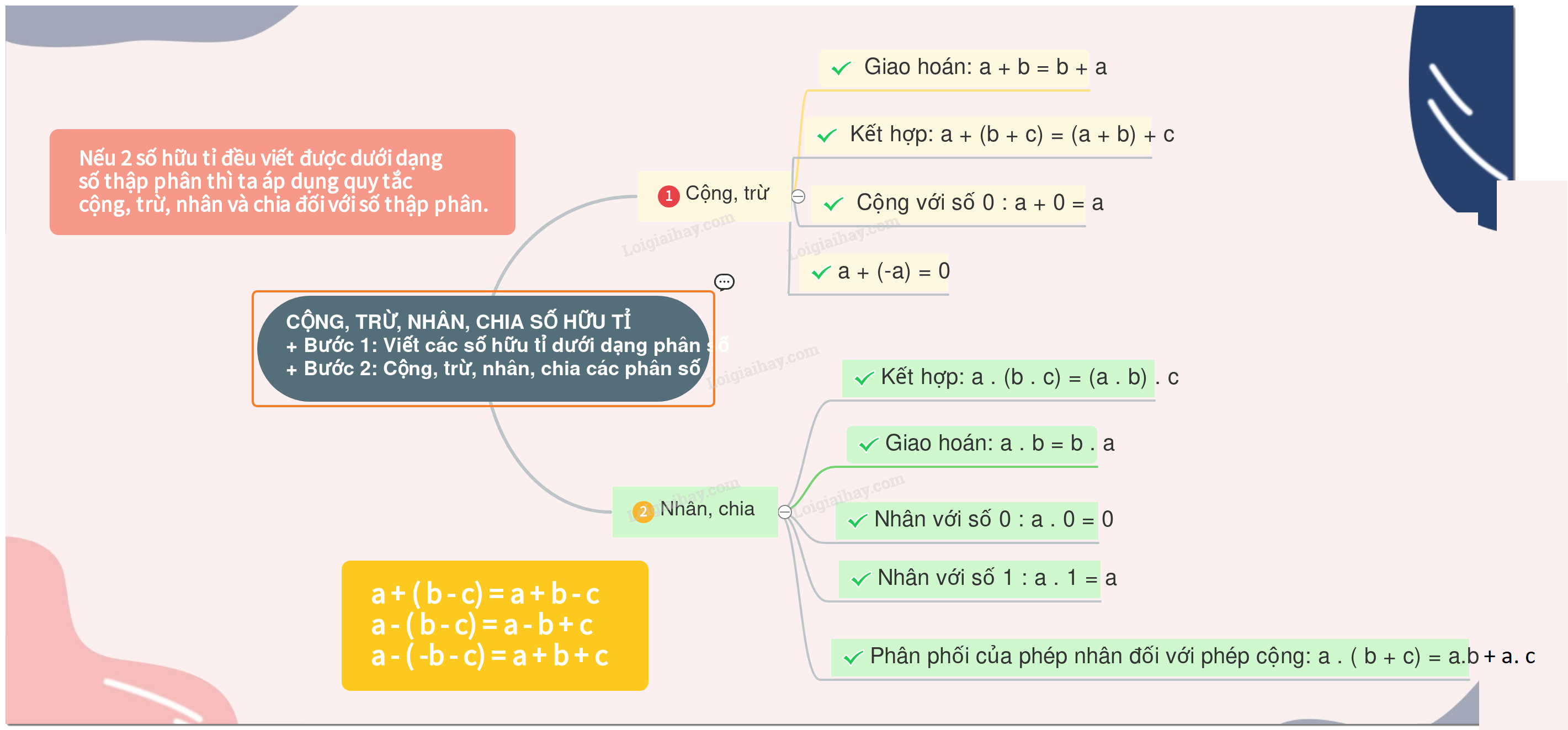
+ Bước 1: Viết các số hữu tỉ dưới dạng phân số
+ Bước 2: Cộng, trừ phân số
Chú ý: Nếu 2 số hữu tỉ đều viết được dưới dạng số thập phân thì ta áp dụng quy tắc cộng và trừ 2 đối với số thập phân.
* Tính chất của phép cộng số hữu tỉ:
+ Giao hoán: a + b = b + a
+ Kết hợp: a + (b + c) = (a + b) + c
+ Cộng với số 0 : a + 0 = a
+ 2 số đối nhau luôn có tổng là 0: a + (-a) = 0
Chú ý: * Trong tập các số hữu tỉ Q, ta cũng có quy tắc dấu ngoặc tương tự như trong tập các số nguyên Z:
Khi bỏ ngoặc,
+ Nếu trước dấu ngoặc có dấu “+” thì ta bỏ ngoặc và giữ nguyên dấu của tất cả các số hạng trong ngoặc.
+ Nếu trước dấu ngoặc có dấu “-” thì ta bỏ ngoặc và đổi dấu tất cả các số hạng trong ngoặc.
* Đối với 1 tổng, ta có thể đổi chỗ tùy ý các số hạng, đặt dấu ngoặc để nhóm các số hạng 1 cách tùy ý.
Ví dụ:
\(\begin{array}{l}\frac{8}{5} - (\frac{5}{4} + \frac{3}{5} - \frac{1}{4})\\ = \frac{8}{5} - \frac{5}{4} - \frac{3}{5} + \frac{1}{4}\\ = \left( {\frac{8}{5} - \frac{3}{5}} \right) + \left( {\frac{1}{4} - \frac{5}{4}} \right)\\ = \frac{5}{5} + \frac{{ - 4}}{4}\\ = 1 + ( - 1)\\ = 0\end{array}\)
2. Nhân hai số hữu tỉ
+ Bước 1: Viết hai số hữu tỉ dưới dạng phân số
+ Bước 2: Nhân hai phân số:
\(\frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}(b,d \ne 0)\)
Chú ý: Nếu 2 số hữu tỉ đều viết được dưới dạng số thập phân thì ta áp dụng quy tắc nhân đối với số thập phân.
3. Tính chất của phép nhân số hữu tỉ:
+ Giao hoán: a . b = b . a
+ Kết hợp: a . (b . c) = (a . b) . c
+ Nhân với số 0 : a . 0 = 0
+ Nhân với số 1 : a . 1 = a
+ Tính chất phân phối của phép nhân đối với phép cộng: a . ( b + c) = a.b + a.c
4. Chia 2 số hữu tỉ
+ Bước 1: Viết hai số hữu tỉ dưới dạng phân số
+ Bước 2: Nhân hai phân số: \(\frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}}(b,c,d \ne 0)\)
Ví dụ:
\(\begin{array}{l}\frac{4}{7}.\frac{3}{5} - \frac{2}{5}:\frac{7}{{ - 4}}\\ = \frac{4}{7}.\frac{3}{5} - \frac{2}{5}.\frac{{ - 4}}{7}\\ = \frac{4}{7}.\frac{3}{5} + \frac{4}{7}.\frac{2}{5}\\ = \frac{4}{7}.\left( {\frac{3}{5} + \frac{2}{5}} \right)\\ = \frac{4}{7}.1\\ = \frac{4}{7}\end{array}\)
Số hữu tỉ là một khái niệm cơ bản trong toán học, xuất hiện xuyên suốt từ chương trình tiểu học đến trung học phổ thông. Việc nắm vững lý thuyết và các phép toán với số hữu tỉ là nền tảng quan trọng để học tốt các môn học khác như đại số, hình học và các ứng dụng thực tế.
Một số được gọi là số hữu tỉ nếu nó có thể được biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0. Ví dụ: 1/2, -3/4, 5, 0.5 (tương đương với 1/2) đều là số hữu tỉ.
Các phép toán cộng, trừ, nhân, chia số hữu tỉ tuân theo các quy tắc sau:
Để cộng hoặc trừ hai số hữu tỉ, ta cần quy đồng mẫu số của chúng. Sau khi quy đồng, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số chung.
Ví dụ: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Lưu ý: Khi cộng hoặc trừ hai số hữu tỉ có cùng mẫu số, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số.
Để nhân hai số hữu tỉ, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
Ví dụ: 1/2 * 1/3 = 1/6
Để chia hai số hữu tỉ, ta nhân số bị chia với nghịch đảo của số chia.
Ví dụ: 1/2 : 1/3 = 1/2 * 3/1 = 3/2
Các phép toán với số hữu tỉ có các tính chất sau:
Có nhiều cách để so sánh hai số hữu tỉ:
Để củng cố kiến thức về các phép toán với số hữu tỉ, bạn có thể thực hành các bài tập sau:
Số hữu tỉ được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết các phép toán với số hữu tỉ. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.