Chào mừng bạn đến với bài học về Lý thuyết Đại lượng tỉ lệ nghịch trong chương trình Toán 7 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về mối quan hệ tỉ lệ nghịch giữa hai đại lượng.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, và cách áp dụng lý thuyết này vào giải các bài toán thực tế. Hãy sẵn sàng để khám phá thế giới toán học thú vị này!
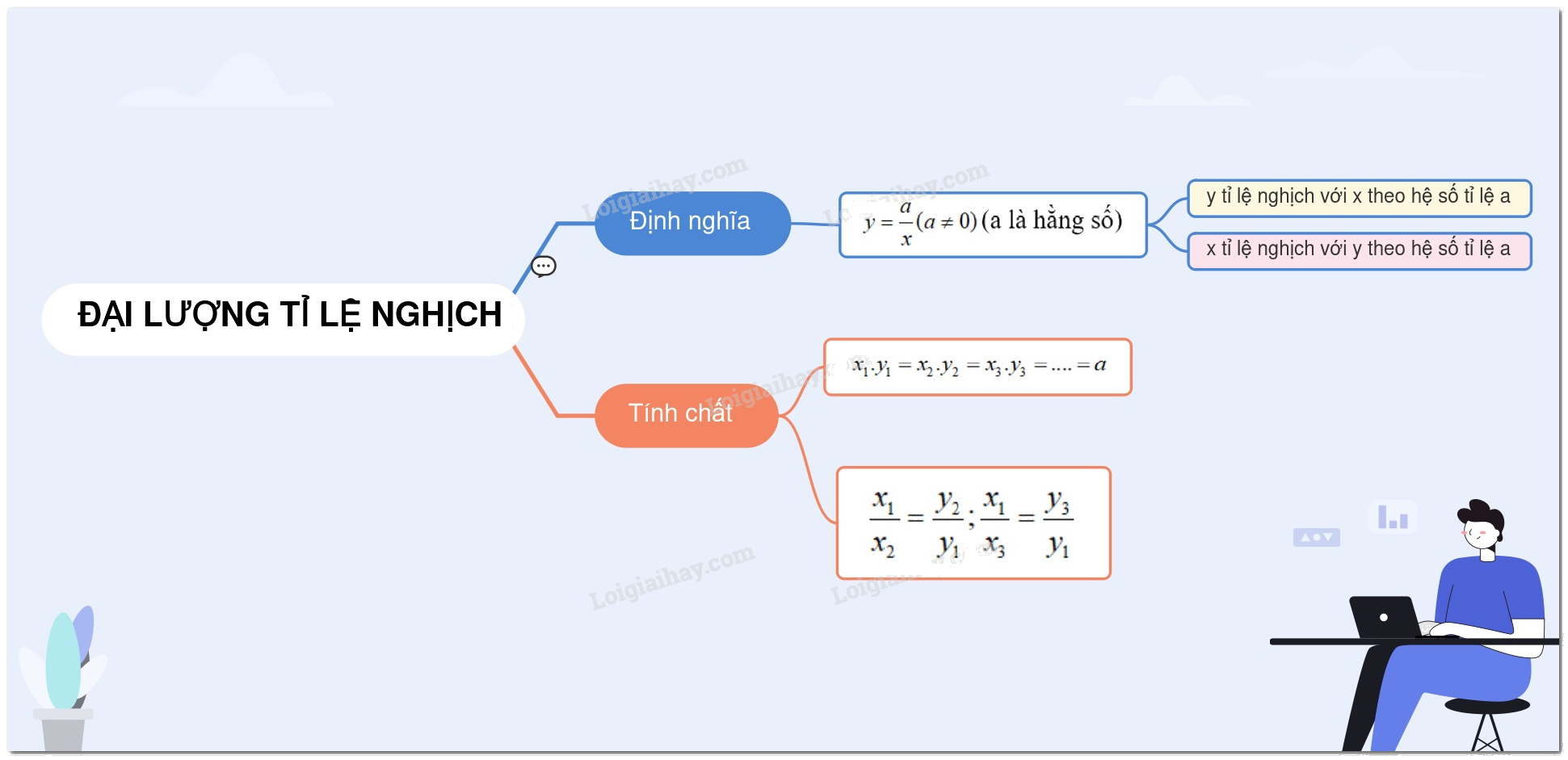
Định nghĩa tỉ lệ nghịch
1. Các kiến thức cần nhớ
Định nghĩa tỉ lệ nghịch
+ Nếu đại lượng $y$ liên hệ với đại lượng $x$ theo công thức \(y = \dfrac{a}{x}\) hay \(xy = a\) (với $a$ là hằng số khác $0$) thì ta nói $y$ tỉ lệ nghịch với $x$ theo hệ số tỉ lệ $a.$
+ Khi đại lượng $y$ tỉ lệ nghịch với đại lượng $x$ thì $x$ cũng tỉ lệ nghịch với $y$ và ta nói hai đại lượng đó tỉ lệ nghịch với nhau.
Ví dụ: Nếu \(y = \dfrac{2}{x}\) thì $y$ tỉ lệ nghịch với $x$ theo hệ số tỉ lệ là $2.$
Chú ý: Khi \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(a\), ta cũng nói \(x\) tỉ lệ nghịch với \(y\) theo hệ số tỉ lệ \(a\)
Tính chất
* Nếu hai đại lượng tỉ lệ nghịch với nhau thì:
+ Tích hai giá trị tương ứng của chúng luôn luôn không đổi.
+ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.
* Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ \(a\) thì:
\({x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a\)
\(\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{{y_2}}}{{{y_1}}};\dfrac{{{x_1}}}{{{x_3}}} = \dfrac{{{y_3}}}{{{y_1}}};...\)
2. Các dạng toán thường gặp
Dạng 1: Bảng giá trị tương ứng của hai đại lượng tỉ lệ nghịch
Phương pháp:
+ Xác định hệ số tỉ lệ \(a.\)
+ Dùng công thức \(y = \dfrac{a}{x}\) hoặc \(x = \dfrac{a}{y}\) để tìm các giá trị tương ứng của $x$ và \(y.\)
Dạng 2: Xét tương quan tỉ lệ nghịch giữa hai đại lượng khi biết bảng các giá trị tương ứng của chúng
Phương pháp:
Xét xem tất cả các tích các giá trị tương ứng của hai đại lượng có bằng nhau không?
Nếu bằng nhau thì hai đại lượng tỉ lệ nghịch.
Nếu không bằng nhau thì hai đại lượng không tỉ lệ nghịch.
Dạng 3: Bài toán về các đại lượng tỉ lệ nghịch
Phương pháp:
+ Xác định rõ các đại lượng có trên đề bài.
+ Xác định tương quan tỉ lệ nghịch giữa hai đại lượng.
+ Áp dụng tính chất về tỉ số các giá trị của hai đại lượng tỉ lệ nghịch và tính chất tỉ lệ thức để giải bài toán.
Dạng 4: Chia một số thành những phần tỉ lệ nghịch với các số cho trước
Phương pháp:
Giả sử chia số $M$ thành ba phần \(x;y;z\) tỉ lệ nghịch với các số \(a,b,c\) cho trước. Ta có
\(ax = by = cz\) hay \(\dfrac{x}{{\dfrac{1}{a}}} = \dfrac{y}{{\dfrac{1}{b}}} = \dfrac{z}{{\dfrac{1}{c}}}.\)
Như vậy để chia số $M$ thành các phần tỉ lệ nghịch với các số \(a,b,c\) (khác \(0\)), ta chỉ cần chia số $M$ thành các phần tỉ lệ thuận với các số \(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\) (đã biết cách làm).
Trong chương trình Toán 7 Chân trời sáng tạo, kiến thức về đại lượng tỉ lệ nghịch đóng vai trò quan trọng, là nền tảng cho các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập liên quan.
Hai đại lượng x và y được gọi là tỉ lệ nghịch với nhau nếu tích xy = a (a là một hằng số khác 0). Hằng số a được gọi là hệ số tỉ lệ. Khi đó, ta có công thức: y = a/x.
Ví dụ 1: Một người đi xe máy với vận tốc v và thời gian t để đi hết quãng đường S không đổi. Mối quan hệ giữa vận tốc và thời gian là mối quan hệ tỉ lệ nghịch. Vì S = v.t, suy ra v = S/t. Nếu vận tốc tăng lên thì thời gian sẽ giảm xuống và ngược lại.
Ví dụ 2: Giá tiền của một sản phẩm và số lượng sản phẩm có thể mua được với một số tiền nhất định là hai đại lượng tỉ lệ nghịch. Nếu giá tiền tăng lên thì số lượng sản phẩm có thể mua được sẽ giảm xuống.
Để nhận biết hai đại lượng x và y tỉ lệ nghịch, ta cần kiểm tra xem tích xy có là một hằng số khác 0 hay không. Nếu xy = a (a ≠ 0) thì x và y tỉ lệ nghịch.
Bài 1: Cho hai đại lượng x và y tỉ lệ nghịch với nhau. Khi x = 2 thì y = 5. Hãy tìm y khi x = -3.
Giải: Vì x và y tỉ lệ nghịch, ta có xy = a. Thay x = 2 và y = 5 vào, ta được 2.5 = a, suy ra a = 10. Vậy y = 10/x. Khi x = -3, ta có y = 10/(-3) = -10/3.
Bài 2: Một đội công nhân cần sửa một đoạn đường. Nếu có 12 công nhân thì hoàn thành công việc trong 5 ngày. Hỏi nếu có 15 công nhân thì hoàn thành công việc trong bao nhiêu ngày?
Giải: Gọi số ngày hoàn thành công việc khi có 15 công nhân là x. Số công nhân và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Ta có 12.5 = 15.x, suy ra x = (12.5)/15 = 4.
Lý thuyết về đại lượng tỉ lệ nghịch có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học. Việc hiểu rõ lý thuyết này giúp chúng ta giải quyết các bài toán thực tế một cách hiệu quả hơn. Các em có thể tìm hiểu thêm về các bài toán liên quan đến tỉ lệ nghịch trong sách giáo khoa và các tài liệu tham khảo khác.
Để củng cố kiến thức về đại lượng tỉ lệ nghịch, các em nên luyện tập thêm nhiều bài tập khác nhau. Các bài tập này có thể được tìm thấy trong sách bài tập, trên các trang web học toán online, hoặc do giáo viên giao.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức cơ bản và quan trọng về Lý thuyết Đại lượng tỉ lệ nghịch Toán 7 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan. Chúc các em học tốt!