Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 77, 78 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 7 và đạt kết quả tốt nhất trong học tập.
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Phương pháp giải:
- Từ các đỉnh ta vẽ các đường cao của tam giác chúng giao nhau ở đâu thì đó là trực tâm
Lời giải chi tiết:
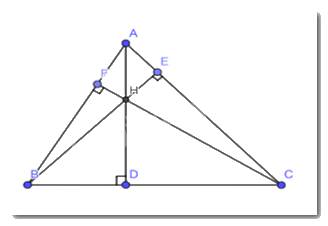
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Phương pháp giải:
- Ta sử dụng êke vẽ 3 đường cao của tam giác
- Sau đó nhận xét về các giao điểm của những đường cao ấy
Lời giải chi tiết:
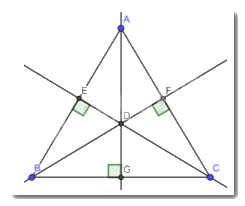
Nhận xét: Các đường cao cùng đi qua 1 điểm
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Phương pháp giải:
- Ta sử dụng định lí 3 đường cao của một tam giác cùng đi qua 1 điểm
Lời giải chi tiết:
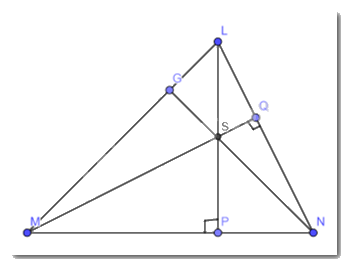
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\( \Rightarrow \)Đường cao từ đỉnh N cũng đi qua S
\( \Rightarrow \)NS là đường cao của tam giác MNL
\( \Rightarrow \) NS vuông góc với ML tại G (là chân đường cao)
Video hướng dẫn giải
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Phương pháp giải:
- Ta sử dụng êke vẽ 3 đường cao của tam giác
- Sau đó nhận xét về các giao điểm của những đường cao ấy
Lời giải chi tiết:
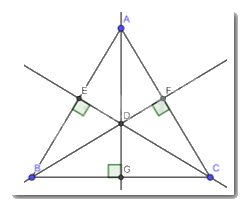
Nhận xét: Các đường cao cùng đi qua 1 điểm
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Phương pháp giải:
- Ta sử dụng định lí 3 đường cao của một tam giác cùng đi qua 1 điểm
Lời giải chi tiết:
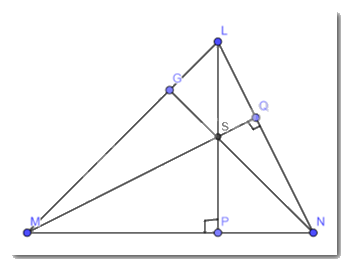
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\( \Rightarrow \)Đường cao từ đỉnh N cũng đi qua S
\( \Rightarrow \)NS là đường cao của tam giác MNL
\( \Rightarrow \) NS vuông góc với ML tại G (là chân đường cao)
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Phương pháp giải:
- Từ các đỉnh ta vẽ các đường cao của tam giác chúng giao nhau ở đâu thì đó là trực tâm
Lời giải chi tiết:
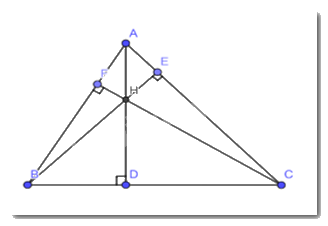
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
Mục 2 của chương trình Toán 7 tập 2 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức đã học về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức để rút gọn biểu thức, tìm giá trị của biểu thức tại một giá trị cụ thể của biến, hoặc giải các bài toán thực tế liên quan đến đa thức.
Bài tập trong mục 2 trang 77, 78 SGK Toán 7 tập 2 Chân trời sáng tạo bao gồm các dạng bài tập sau:
a) (3x + 5y) + (5x - 2y)
Lời giải: (3x + 5y) + (5x - 2y) = 3x + 5y + 5x - 2y = (3x + 5x) + (5y - 2y) = 8x + 3y
b) (x2 - 2x + 1) - (x2 + x - 3)
Lời giải: (x2 - 2x + 1) - (x2 + x - 3) = x2 - 2x + 1 - x2 - x + 3 = (x2 - x2) + (-2x - x) + (1 + 3) = -3x + 4
a) 2x + 3y khi x = 1, y = -1
Lời giải: 2x + 3y = 2(1) + 3(-1) = 2 - 3 = -1
b) x2 - 2x + 1 khi x = -2
Lời giải: x2 - 2x + 1 = (-2)2 - 2(-2) + 1 = 4 + 4 + 1 = 9
Ngoài SGK Toán 7 tập 2 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin giải quyết các bài tập mục 2 trang 77, 78 SGK Toán 7 tập 2 Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!