Chào mừng bạn đến với bài học về Lý thuyết Góc ở vị trí đặc biệt trong chương trình SGK Toán 7 - Chân trời sáng tạo. Đây là một phần kiến thức quan trọng, đặt nền móng cho các bài học hình học phức tạp hơn ở các lớp trên.
Bài học này sẽ giúp bạn hiểu rõ các khái niệm về góc kề bù, góc so le trong, góc đồng vị, góc trong so le, góc ngoài và cách áp dụng chúng vào giải các bài tập thực tế.
1. 2 góc kề bù
1. 2 góc kề bù
Hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
* Tính chất: 2 góc kề bù có tổng số đo là 180 độ.
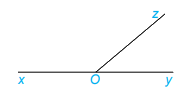
Góc xOz và góc yOz là 2 góc kề bù vì có tia Oz chung; tia Ox và Oy là 2 tia đối nhau.
Ta có: \(\widehat {xOz} + \widehat {yOz} = 180^\circ \)
Chú ý:
Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa 2 tia Ox và Oy. Khi đó:
\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\)
2. 2 góc đối đỉnh
2 góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
* Tính chất: Hai góc đối đỉnh thì bằng nhau
Chú ý: 2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
Ví dụ:
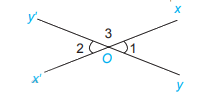
\(\widehat {{O_1}} = \widehat {{O_2}};\widehat {{O_3}} = \widehat {{O_4}}\)( đối đỉnh)
Chú ý: 2 đường thẳng cắt nhau và trong các góc tạo thành có một góc vuông thì 2 đường thẳng đó vuông góc.
Ví dụ:
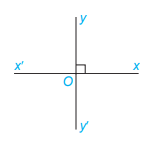
Hai đường thẳng xx' và yy' cắt nhau tại O, tạo thành 1 góc vuông. Ta nói hai đường thẳng xx' và yy' vuông góc với nhau.
Kí hiệu: xx' \(\bot\) yy' hoặc yy' \(\bot\) xx'
Trong chương trình Toán 7, việc nắm vững kiến thức về góc và các mối quan hệ giữa chúng là vô cùng quan trọng. Bài viết này sẽ trình bày chi tiết lý thuyết về các góc ở vị trí đặc biệt, dựa trên nội dung SGK Toán 7 - Chân trời sáng tạo, giúp học sinh hiểu rõ và áp dụng hiệu quả vào giải bài tập.
Trước khi đi sâu vào các góc ở vị trí đặc biệt, chúng ta cần ôn lại một số khái niệm cơ bản:
Hai góc kề bù là hai góc có chung cạnh, không có điểm chung ngoài cạnh chung và tổng số đo hai góc bằng 180 độ. Ví dụ, góc xOy và góc yOz là hai góc kề bù nếu chúng có chung cạnh Oy và xOy + yOz = 180 độ.
Khi một đường thẳng cắt hai đường thẳng phân biệt, ta có các loại góc sau:
Trong SGK Toán 7 - Chân trời sáng tạo, các em sẽ được làm quen với tính chất quan trọng: Nếu một đường thẳng cắt hai đường thẳng song song thì:
Góc trong so le là hai góc nằm bên trong hai đường thẳng và ở hai phía đối diện của đường thẳng cắt. Đây là một trường hợp đặc biệt của góc so le trong.
Góc ngoài của một tam giác là góc tạo bởi một cạnh của tam giác và đường thẳng kéo dài cạnh đối diện. Tính chất quan trọng: Góc ngoài của một tam giác bằng tổng hai góc trong không kề với góc ngoài đó.
Để hiểu rõ hơn về lý thuyết, chúng ta hãy xem xét một số bài tập vận dụng:
Lý thuyết về các góc ở vị trí đặc biệt không chỉ quan trọng trong chương trình học mà còn có ứng dụng rộng rãi trong thực tế, như trong kiến trúc, xây dựng, hàng hải,... Việc hiểu rõ các khái niệm và tính chất này sẽ giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả.
Bài viết này đã trình bày chi tiết lý thuyết về các góc ở vị trí đặc biệt trong SGK Toán 7 - Chân trời sáng tạo. Hy vọng rằng, thông qua bài viết này, các em học sinh sẽ nắm vững kiến thức và áp dụng thành công vào giải các bài tập. Chúc các em học tốt!