Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 7 tập 2, chương trình Chân trời sáng tạo.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2, trang 49, 50, 51, 52, 53, và 54. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước: -Vẽ đoạn thẳng B’C’= BC -Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA. -Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung) -Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b) Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt
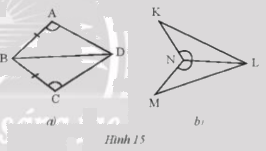
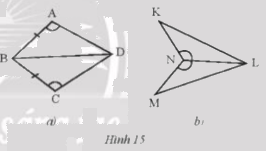
Nêu thêm điều kiện để hai tam giác trong mỗi hình bên (Hình 15a,b) bằng nhau theo trường hợp cạnh – góc – cạnh.
Phương pháp giải:
Dựa vào trường hợp cạnh – góc – cạnh
Lời giải chi tiết:
a) Theo trường hợp cạnh – góc – cạnh ta cần AD = CD để 2 tam giác bằng nhau
b) Theo trường hợp cạnh – góc – cạnh ta cần KN = MN để 2 tam giác bằng nhau
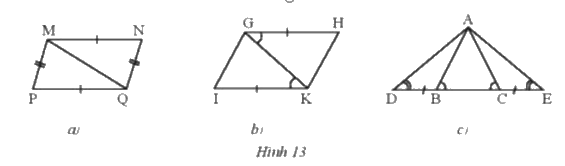
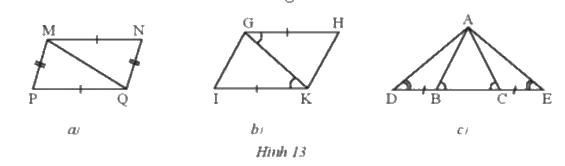
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
Phương pháp giải:
Dựa vào các trường hợp 2 tam giác bằng nhau c-c-c; c-g-c; g-c-g
Lời giải chi tiết:
a) Ta thấy tam giác MNQ = tam giác MPQ ( c-c-c )
b) Ta thấy tam giác GHK = tam giác GIK ( c-g-c )
c) Ta thấy tam giác ADB = tam giác ACE ( g-c-g )
Tam giác ADC = tam giác AEB ( g-c-g )
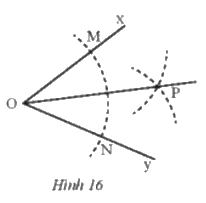
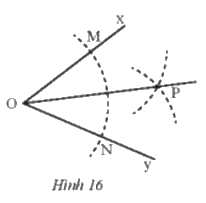
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
Phương pháp giải:
- Ta chứng minh 2 tam giác bằng nhau bằng phương pháp cạnh – cạnh – cạnh
Lời giải chi tiết:
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
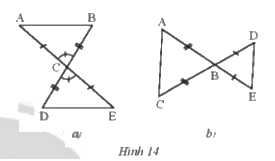
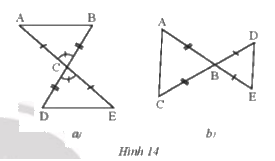
Hai tam giác trong mỗi hình bên (Hình 14a,b) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g
Lời giải chi tiết:
a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:
AC = CE
\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )
CB = CD
\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)
b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì
\(AC \ne BE;BC \ne BD;DE \ne AC\)
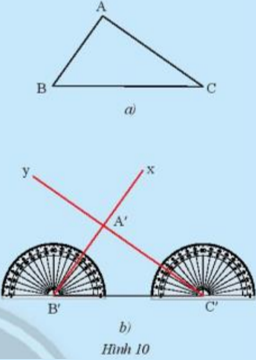
Cho tam giác ABC như trong Hình 10a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có B’C’ = BC, \(\widehat {B'} = \widehat B\), \(\widehat {C'} = \widehat C\)theo các bước:
-Vẽ đoạn thẳng B’C’ = BC.
-Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’vẽ \(\widehat {C'B'x} = \widehat {CBA}\), và vẽ \(\widehat {B'C'y} = \widehat {BCA}\).
-Vẽ giao điểm A’của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
- Ta vẽ đoạn thẳng trước rồi từ 2 đầu đoạn thẳng lần lượt vẽ các góc theo số đo của tam giác ABC
- Sau khi cắt và chồng lên nhau sẽ thu được kết quả
Lời giải chi tiết:
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Từ đó ta suy ra 2 tam giác bằng nhau khi có 2 góc bằng nhau và cạnh xen giữa 2 góc đó cũng bằng nhau
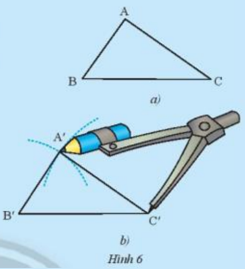
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước:
-Vẽ đoạn thẳng B’C’= BC
-Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA.
-Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung)
-Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b)
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
Vẽ hình và so sánh độ dài các cạnh các góc của 2 tam giác
Lời giải chi tiết:
Xét tam giác ABC và tam giác A’B’C’ có :
BC = B’C’ ( giả thiết )
B’A’ = BA
A’C’ = CA
Hai tam giác có thể đặt chồng khít lên nhau nên 2 tam giác bằng nhau
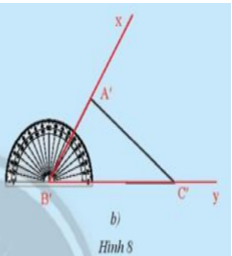
Cho tam giác ABC như trong Hình 8a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có \(\widehat {B'} = \widehat B\), B’A’ = BA, B’C’ = BC theo các bước:
- Vẽ \(\widehat {xB'y} = \widehat {ABC}\)
- Trên tia B’x lấy đoạn B’A’= BA.
- Trên tia B’y lấy đoạn B’C’ = BC.
-Vẽ đoạn A’C’, ta được tam giác A’B’C’(Hình 8b)
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
- Vẽ góc trước rồi vẽ 2 cạnh theo đề bài
- Cắt giấy theo hình vẽ được
- So sánh hai tam giác xem chúng bằng nhau hay không
Lời giải chi tiết:
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Chú ý: 2 tam giác bằng nhau khi có 2 cặp cạnh bằng nhau và góc xen giữa 2 cặp cạnh đó cũng bằng nhau .
Video hướng dẫn giải
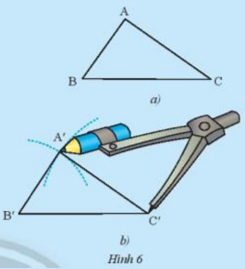
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước:
-Vẽ đoạn thẳng B’C’= BC
-Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA.
-Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung)
-Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b)
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
Vẽ hình và so sánh độ dài các cạnh các góc của 2 tam giác
Lời giải chi tiết:
Xét tam giác ABC và tam giác A’B’C’ có :
BC = B’C’ ( giả thiết )
B’A’ = BA
A’C’ = CA
Hai tam giác có thể đặt chồng khít lên nhau nên 2 tam giác bằng nhau
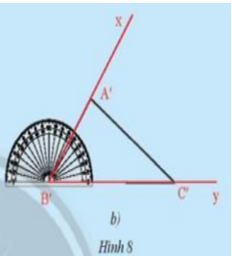
Cho tam giác ABC như trong Hình 8a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có \(\widehat {B'} = \widehat B\), B’A’ = BA, B’C’ = BC theo các bước:
- Vẽ \(\widehat {xB'y} = \widehat {ABC}\)
- Trên tia B’x lấy đoạn B’A’= BA.
- Trên tia B’y lấy đoạn B’C’ = BC.
-Vẽ đoạn A’C’, ta được tam giác A’B’C’(Hình 8b)
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
- Vẽ góc trước rồi vẽ 2 cạnh theo đề bài
- Cắt giấy theo hình vẽ được
- So sánh hai tam giác xem chúng bằng nhau hay không
Lời giải chi tiết:
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Chú ý: 2 tam giác bằng nhau khi có 2 cặp cạnh bằng nhau và góc xen giữa 2 cặp cạnh đó cũng bằng nhau .
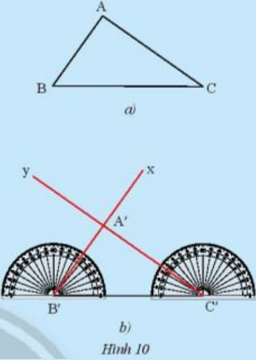
Cho tam giác ABC như trong Hình 10a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có B’C’ = BC, \(\widehat {B'} = \widehat B\), \(\widehat {C'} = \widehat C\)theo các bước:
-Vẽ đoạn thẳng B’C’ = BC.
-Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’vẽ \(\widehat {C'B'x} = \widehat {CBA}\), và vẽ \(\widehat {B'C'y} = \widehat {BCA}\).
-Vẽ giao điểm A’của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Phương pháp giải:
- Ta vẽ đoạn thẳng trước rồi từ 2 đầu đoạn thẳng lần lượt vẽ các góc theo số đo của tam giác ABC
- Sau khi cắt và chồng lên nhau sẽ thu được kết quả
Lời giải chi tiết:
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Từ đó ta suy ra 2 tam giác bằng nhau khi có 2 góc bằng nhau và cạnh xen giữa 2 góc đó cũng bằng nhau
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
Phương pháp giải:
Dựa vào các trường hợp 2 tam giác bằng nhau c-c-c; c-g-c; g-c-g
Lời giải chi tiết:
a) Ta thấy tam giác MNQ = tam giác MPQ ( c-c-c )
b) Ta thấy tam giác GHK = tam giác GIK ( c-g-c )
c) Ta thấy tam giác ADB = tam giác ACE ( g-c-g )
Tam giác ADC = tam giác AEB ( g-c-g )
Hai tam giác trong mỗi hình bên (Hình 14a,b) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g
Lời giải chi tiết:
a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:
AC = CE
\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )
CB = CD
\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)
b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì
\(AC \ne BE;BC \ne BD;DE \ne AC\)
Nêu thêm điều kiện để hai tam giác trong mỗi hình bên (Hình 15a,b) bằng nhau theo trường hợp cạnh – góc – cạnh.
Phương pháp giải:
Dựa vào trường hợp cạnh – góc – cạnh
Lời giải chi tiết:
a) Theo trường hợp cạnh – góc – cạnh ta cần AD = CD để 2 tam giác bằng nhau
b) Theo trường hợp cạnh – góc – cạnh ta cần KN = MN để 2 tam giác bằng nhau
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
Phương pháp giải:
- Ta chứng minh 2 tam giác bằng nhau bằng phương pháp cạnh – cạnh – cạnh
Lời giải chi tiết:
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
Mục 2 của chương trình Toán 7 tập 2 Chân trời sáng tạo tập trung vào các kiến thức về biểu thức đại số, bao gồm các khái niệm như biến, hằng số, biểu thức, và giá trị của biểu thức. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Các bài tập trang 49 chủ yếu yêu cầu học sinh viết các biểu thức đại số dựa trên các tình huống thực tế. Ví dụ, bài 1 yêu cầu viết biểu thức tính diện tích hình chữ nhật khi biết chiều dài và chiều rộng. Bài 2 yêu cầu viết biểu thức tính chu vi hình tròn khi biết bán kính. Để giải các bài tập này, học sinh cần hiểu rõ ý nghĩa của các biến và hằng số, cũng như các phép toán cơ bản.
Trang 50 tập trung vào việc tính giá trị của biểu thức khi biết giá trị của các biến. Ví dụ, bài 3 yêu cầu tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1. Để giải bài tập này, học sinh cần thay thế các giá trị của biến vào biểu thức và thực hiện các phép toán theo đúng thứ tự ưu tiên.
Các bài tập từ trang 51 đến trang 52 yêu cầu học sinh vận dụng kiến thức về biểu thức đại số để giải các bài toán thực tế. Ví dụ, bài 4 yêu cầu tính số tiền phải trả khi mua một số lượng hàng hóa với giá tiền đơn vị cho trước. Bài 5 yêu cầu tính diện tích và chu vi của một hình chữ nhật khi biết chiều dài và chiều rộng. Để giải các bài tập này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan, và xây dựng biểu thức đại số phù hợp.
Các bài tập trang 53 và 54 là các bài tập nâng cao, đòi hỏi học sinh phải có khả năng tư duy logic và sáng tạo. Ví dụ, bài 6 yêu cầu chứng minh một đẳng thức đại số. Bài 7 yêu cầu giải một bài toán tìm x. Để giải các bài tập này, học sinh cần nắm vững các quy tắc biến đổi đại số và sử dụng các phương pháp giải toán phù hợp.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho tất cả các bài tập trong mục 2, trang 49, 50, 51, 52, 53, và 54. Lời giải được trình bày một cách rõ ràng, dễ hiểu, kèm theo các giải thích chi tiết về các bước thực hiện. Ngoài ra, chúng tôi cũng cung cấp các bài tập tương tự để học sinh có thể luyện tập và củng cố kiến thức.
Hy vọng rằng với sự hỗ trợ của giaitoan.edu.vn, các em học sinh sẽ học tốt môn Toán 7 và đạt được kết quả cao trong học tập. Chúc các em thành công!
| Bài tập | Nội dung |
|---|---|
| Bài 1 (trang 49) | Viết biểu thức tính diện tích hình chữ nhật |
| Bài 2 (trang 50) | Tính giá trị của biểu thức 3x + 2y |
| Bài 3 (trang 51) | Giải bài toán thực tế về mua hàng |