Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 72, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 3 trang 72 nhé!
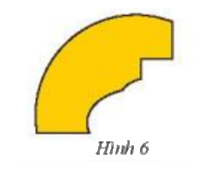
Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình 6). Làm thế nào để các định được bán kính của đĩa cổ này?
Đề bài
Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình 6). Làm thế nào để các định được bán kính của đĩa cổ này?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Sử dụng tính chất của điểm giao 2 trung trực trong tam giác
Lời giải chi tiết
Gọi O là tâm của chiếc đĩa
\( \Rightarrow \) OA = OB = OC = r ( do cùng có độ dài = bán kính )
Xét tam giác ABC có O là điểm cách đều A, B, C
\( \Rightarrow \) O là giao của 3 đường trung trực tam giác ABC
Để xác định O ta vẽ 2 đường trung trực của AB, BC chúng cắt nhau tại O .
Bài 3 trang 72 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học về các góc và mối quan hệ giữa các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Bài tập này yêu cầu học sinh vận dụng kiến thức về góc so le trong, góc đồng vị, góc trong cùng phía để chứng minh tính chất của các góc.
Bài 3 bao gồm một hình vẽ và yêu cầu học sinh chứng minh một số cặp góc bằng nhau hoặc bù nhau dựa trên các tính chất đã học. Để giải bài tập này, học sinh cần:
Đề bài: (Hình vẽ đi kèm)
Cho hình vẽ, biết a // b. Chứng minh:
Lời giải:
1. Chứng minh ∠A1 = ∠B1:
Vì a // b nên ∠A1 và ∠B1 là hai góc so le trong. Do đó, ∠A1 = ∠B1 (tính chất hai đường thẳng song song).
2. Chứng minh ∠A1 + ∠B2 = 180°:
Vì a // b nên ∠A1 và ∠B2 là hai góc trong cùng phía. Do đó, ∠A1 + ∠B2 = 180° (tính chất hai đường thẳng song song).
Để củng cố kiến thức về các góc và mối quan hệ giữa chúng, bạn có thể thực hành thêm các bài tập tương tự. Ví dụ:
Khi giải các bài tập về góc, bạn cần chú ý:
Bài 3 trang 72 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các góc và mối quan hệ giữa chúng. Hy vọng với lời giải chi tiết và những lưu ý trên, bạn sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự trong tương lai. Chúc bạn học tốt!
| Góc | Tính chất |
|---|---|
| Góc so le trong | ∠A1 = ∠B1 |
| Góc đồng vị | ∠A1 = ∠B1 |
| Góc trong cùng phía | ∠A1 + ∠B2 = 180° |