Chào mừng bạn đến với bài học về Lý thuyết Số thực và Giá trị tuyệt đối của số thực, một phần quan trọng trong chương trình Toán 7 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về số thực và cách xác định giá trị tuyệt đối của chúng.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu cùng với các bài tập thực hành đa dạng để bạn có thể tự tin chinh phục môn Toán.
1. Số thực và tập hợp các số thực
1. Số thực và tập hợp các số thực
* Số hữu tỉ và số vô tỉ gọi chung là số thực.
* Tập hợp các số thực được kí hiệu là R.
Chú ý: + Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
2. Thứ tự trong tập hợp các số thực
So sánh 2 số thực:
* Các số thực đều viết được dưới dạng số thập phân ( hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.
Ví dụ:
0,322 … < 0,324… nên 0,3(2) < 0,324…
* Với 2 số thực bất kì, ta luôn có hoặc a = b hoặc a > b hoặc a < b
* Nếu a < b ; b < c thì a < c ( Tính chất bắc cầu)
* Nếu a < b thì điểm a nằm trước điểm b trên trục số
Chú ý: Nếu 0 < a < b thì \(\sqrt a < \sqrt b \)
Ví dụ: Vì 3 < 4 nên \(\sqrt 3 < \sqrt 4 = 2\)
3. Trục số thực
+ Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
* Trục số thực được biểu diễn bởi 1 số điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Chú ý: Các số thực lấp đầy trục số.
4. Số đối của một số thực
Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này là số đối của số kia.
Số đối của số thực x là –x. Ta có: x + (-x) = 0
Ví dụ: Số đối của \( - \sqrt 8 \) là \(\sqrt 8 \)
Chú ý: Nếu a > b thì –a < -b
5. Giá trị tuyệt đối của một số thực
Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là |a|
Nhận xét:
+ Hai số đối nhau thì có giá trị tuyệt đối bằng nhau
+ Giá trị tuyệt đối của 0 là 0
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
+ Giá trị tuyệt đối của một số thực luôn không âm.
Ví dụ: |2,3| = 2,3
|-2,3| = 2,3
|-2,3| = |2,3|
Chú ý: Giả sử 2 điểm A và B lần lượt biểu diễn 2 số thực a và b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là | a – b|
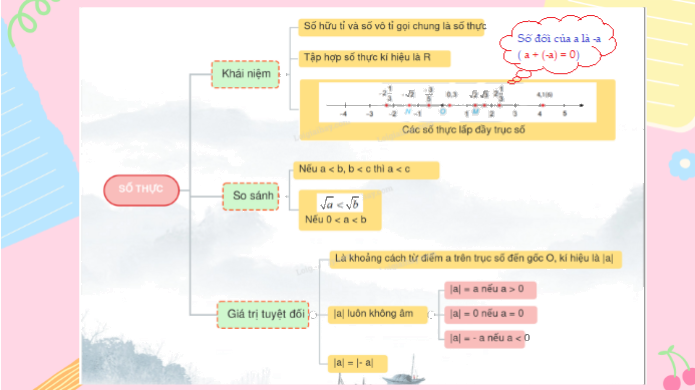
Trong chương trình Toán 7, việc nắm vững kiến thức về số thực và giá trị tuyệt đối là vô cùng quan trọng. Đây là nền tảng để học sinh có thể tiếp cận các khái niệm toán học phức tạp hơn ở các lớp trên. Bài viết này sẽ trình bày chi tiết về lý thuyết số thực, giá trị tuyệt đối của số thực theo chương trình SGK Toán 7 - Chân trời sáng tạo.
Số thực bao gồm tập hợp các số hữu tỉ và số vô tỉ.
Tập hợp số thực được ký hiệu là ℝ.
Mỗi số thực đều có thể được biểu diễn bằng một điểm trên trục số. Trục số là một đường thẳng, trên đó ta chọn một điểm làm gốc (thường là số 0), một chiều dương và một đơn vị đo.
Số thực dương nằm bên phải gốc, số thực âm nằm bên trái gốc.
Giá trị tuyệt đối của một số thực x, ký hiệu là |x|, là khoảng cách từ điểm biểu diễn của x trên trục số đến điểm gốc.
Công thức tính giá trị tuyệt đối:
Ví dụ:
Giá trị tuyệt đối có một số tính chất quan trọng:
Bài 1: Tính giá trị tuyệt đối của các số sau: -7, 2.5, 0, -1/3
Bài 2: So sánh |−5| và |3|
Bài 3: Tìm x biết |x| = 4
Giá trị tuyệt đối được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học, ví dụ như:
Hi vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết số thực và giá trị tuyệt đối của số thực. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan. Chúc bạn học tốt!