Chào mừng các em học sinh đến với lời giải chi tiết Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo. Bài học này tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, giúp các em hiểu sâu hơn về môn Toán.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và đầy đủ nhất, hỗ trợ các em trong quá trình học tập và ôn luyện.
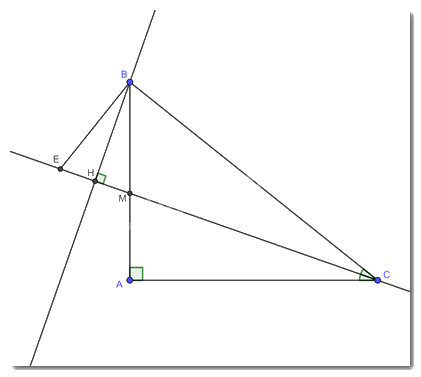
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
Đề bài
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)
c) Chứng minh rằng \(EB \bot BC\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a)Ta chứng minh \(\Delta \)BME có 2 cạnh bên hoặc 2 góc đáy bằng nhau thông qua việc chứng minh 2 tam giác EHB và MHB bằng nhau.
b)Ta chứng minh \(\widehat {EBH} = \widehat {ACM}\)do cùng = \(\widehat {MBH}\)
c)Ta chứng minh\(\widehat {EBH} + \widehat {BCE} = {90^o}\)
Lời giải chi tiết
a)Xét \(\Delta \)BHE và \(\Delta \)BHM có :
BH là cạnh chung
EH = HM (do M đối xứng E qua H)
\(\widehat {BHE} = \widehat {BHM} = {90^o}\)
\( \Rightarrow \)\(\Delta \)BHE = \(\Delta \)BHM (c-g-c)
\( \Rightarrow \)BM = BE (cạnh tương ứng)
và \(\widehat {EBH} = \widehat {MBH}\)(góc tương ứng) (1)
\( \Rightarrow \)\(\Delta \)BEM cân tại B (2 cạnh bên bằng nhau)
b)Xét \(\Delta \)BHM vuông tại H \( \Rightarrow \widehat {BMH} + \widehat {MBH} = {90^o}\)
Xét \(\Delta \)AMC vuông tại A \( \Rightarrow \widehat {AMC} + \widehat {MCA} = {90^o}\)
Mà \(\widehat {HMB} = \widehat {AMC}\)(2 góc đối đỉnh)
\( \Rightarrow \widehat {MCA} = \widehat {MBH} = {90^o} - \widehat {AMC} = {90^o} - \widehat {HMB}\)(2)
Từ (1) và (2) \( \Rightarrow \widehat {EBH} = \widehat {ACM}\)
c)Vì \(\widehat {BCM} = \widehat {ACM}\) (do CM là phân giác góc C)
\( \Rightarrow \widehat {EBH} = \widehat {BCM}\)(cùng bằng \(\widehat {AMC}\)) (3)
Xét \(\Delta \)EHB vuông tại H có \(\widehat {EBH} + \widehat {BEH} = {90^o}\)(4)
Từ (3) và (4) \( \Rightarrow \widehat {BCM} + \widehat {BEH} = {90^o}\)
\( \Rightarrow \widehat {EBC} = {90^o} \Rightarrow EB \bot BC\)
Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố kiến thức về các phép toán cơ bản, các tính chất của số tự nhiên, số nguyên, phân số và các biểu thức đại số đơn giản. Mục tiêu chính của bài học là giúp học sinh rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Bài 9 bao gồm các dạng bài tập khác nhau, từ việc thực hiện các phép tính đơn giản đến việc giải các bài toán có tính ứng dụng cao. Cụ thể, bài tập thường bao gồm:
Để tính giá trị của biểu thức, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau) và các tính chất của số. Ví dụ, để tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2, ta thay x = 1 và y = 2 vào biểu thức và thực hiện các phép tính:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Để giải phương trình đơn giản, học sinh cần thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = a (với a là một số cụ thể). Ví dụ, để giải phương trình x + 5 = 10, ta trừ cả hai vế của phương trình cho 5:
x + 5 - 5 = 10 - 5
x = 5
Bài tập này tương tự như giải phương trình, nhưng yêu cầu học sinh phải tìm x dựa trên một biểu thức cho trước. Ví dụ, để tìm x biết 3x - 2 = 7, ta cộng cả hai vế của phương trình cho 2:
3x - 2 + 2 = 7 + 2
3x = 9
Sau đó, ta chia cả hai vế của phương trình cho 3:
x = 9 / 3
x = 3
Đây là dạng bài tập đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các tình huống thực tế. Ví dụ, một bài toán có thể yêu cầu tính diện tích của một mảnh đất hình chữ nhật, hoặc tính số tiền lãi khi gửi tiết kiệm. Để giải quyết các bài toán này, học sinh cần phân tích đề bài, xác định các yếu tố cần thiết và áp dụng các công thức phù hợp.
Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài học quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.