Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 1 - Chân trời sáng tạo. Mục 2 trang 60 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và phương pháp giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải đáp này với mục tiêu giúp các em học sinh tự tin hơn trong quá trình học tập.
Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như ở Hình 3b
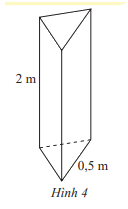
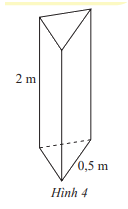
Tính diện tích xung quanh của một cột bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).
Phương pháp giải:
Diện tích xung quanh lăng trụ đứng = chu vi đáy. chiều cao
Lời giải chi tiết:
Diện tích xung quanh của cột bê tông đó là:
Sxq = Cđáy . h = (0,5 + 0,5 +0,5). 2 = 3 (m2)
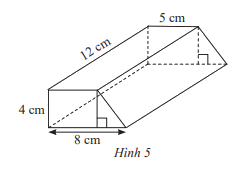
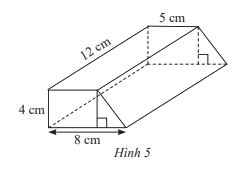
Tính thể tích hình lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5
Phương pháp giải:
Thể tích hình lăng trụ là: V = Diện tích đáy . chiều cao
Diện tích hình thang có 2 đáy là a và b, chiều cao h là: S = (a+b).h : 2
Lời giải chi tiết:
Diện tích đáy của lăng trụ là:
Sđáy = (5+8).4:2 = 26 (cm2)
Thể tích hình lăng trụ đứng trong Hình 5 là:
V = Sđáy . h = 26 . 12 = 312 (cm3)
Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như ở Hình 3b
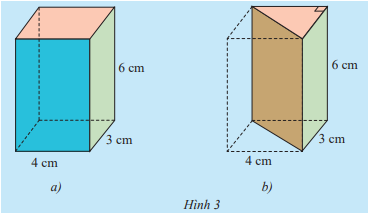
a) Tính thể tích của hình hộp chữ nhật.
b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
c) Gọi Sđáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ tam giác. Hãy tính Sđáy . h
d) So sánh Sđáy . h và kết quả dự đoán ở câu b.
Phương pháp giải:
Thể tích của hình hộp chữ nhật có chiều dài đáy a, chiều rộng b, chiều cao c là: V = a.b.c
Diện tích hình chữ nhật có chiều dài a, chiều rộng b là: S = a.b
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật là: V = 4.3.6 = 72 (cm3)
b) Vì hình hộp cắt đi một nửa thì được hình lăng trụ đứng nên dự đoán thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật ở câu a.
c) Sđáy = 4.3:2 = 6 (cm2)
Sđáy . h = 6.6 = 36 (cm3)
d) Sđáy . h = 36 = \(\frac {1}{2}\). 72 = \(\frac {1}{2}\).Vhình hộp
Vậy Sđáy . h và kết quả dự đoán ở câu b là như nhau.
Video hướng dẫn giải
Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như ở Hình 3b
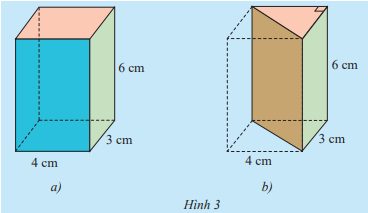
a) Tính thể tích của hình hộp chữ nhật.
b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
c) Gọi Sđáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ tam giác. Hãy tính Sđáy . h
d) So sánh Sđáy . h và kết quả dự đoán ở câu b.
Phương pháp giải:
Thể tích của hình hộp chữ nhật có chiều dài đáy a, chiều rộng b, chiều cao c là: V = a.b.c
Diện tích hình chữ nhật có chiều dài a, chiều rộng b là: S = a.b
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật là: V = 4.3.6 = 72 (cm3)
b) Vì hình hộp cắt đi một nửa thì được hình lăng trụ đứng nên dự đoán thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật ở câu a.
c) Sđáy = 4.3:2 = 6 (cm2)
Sđáy . h = 6.6 = 36 (cm3)
d) Sđáy . h = 36 = \(\frac {1}{2}\). 72 = \(\frac {1}{2}\).Vhình hộp
Vậy Sđáy . h và kết quả dự đoán ở câu b là như nhau.
Tính diện tích xung quanh của một cột bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).
Phương pháp giải:
Diện tích xung quanh lăng trụ đứng = chu vi đáy. chiều cao
Lời giải chi tiết:
Diện tích xung quanh của cột bê tông đó là:
Sxq = Cđáy . h = (0,5 + 0,5 +0,5). 2 = 3 (m2)
Tính thể tích hình lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5
Phương pháp giải:
Thể tích hình lăng trụ là: V = Diện tích đáy . chiều cao
Diện tích hình thang có 2 đáy là a và b, chiều cao h là: S = (a+b).h : 2
Lời giải chi tiết:
Diện tích đáy của lăng trụ là:
Sđáy = (5+8).4:2 = 26 (cm2)
Thể tích hình lăng trụ đứng trong Hình 5 là:
V = Sđáy . h = 26 . 12 = 312 (cm3)
Mục 2 của chương trình Toán 7 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức cơ bản về số nguyên, số hữu tỉ, và các phép toán trên chúng. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập 1 yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số nguyên. Để giải bài tập này, học sinh cần nhớ rõ quy tắc dấu trong các phép toán. Ví dụ, khi cộng hai số nguyên âm, ta cộng hai giá trị tuyệt đối của chúng và đặt dấu âm trước kết quả.
Khi trừ hai số nguyên, ta thực chất là cộng số trừ với số đối của số bị trừ. Ví dụ, 5 - (-3) = 5 + 3 = 8.
Bài tập 2 tập trung vào việc thực hiện các phép toán cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần quy đồng mẫu số trước khi thực hiện các phép toán cộng và trừ. Khi nhân và chia số hữu tỉ, ta thực hiện như nhân và chia phân số.
Lưu ý: Khi quy đồng mẫu số, ta cần tìm bội chung nhỏ nhất (BCNN) của các mẫu số để đảm bảo tính chính xác của kết quả.
Bài tập 3 yêu cầu học sinh vận dụng kiến thức về số nguyên và số hữu tỉ để giải các bài toán thực tế. Các bài toán này thường liên quan đến việc tính toán tiền bạc, đo lường, hoặc so sánh các đại lượng.
Ví dụ: Một cửa hàng bán một chiếc áo với giá 150.000 đồng và giảm giá 10%. Hỏi giá chiếc áo sau khi giảm giá là bao nhiêu?
Giải: Số tiền giảm giá là 150.000 x 10% = 15.000 đồng. Giá chiếc áo sau khi giảm giá là 150.000 - 15.000 = 135.000 đồng.
Ngoài các bài tập đã nêu trên, mục 2 còn có nhiều dạng bài tập khác, như:
Để giải bài tập Toán 7 tập 1 - Chân trời sáng tạo một cách hiệu quả, học sinh cần:
| Phép toán | Quy tắc |
|---|---|
| Cộng hai số nguyên âm | Cộng hai giá trị tuyệt đối và đặt dấu âm trước kết quả |
| Trừ hai số nguyên | Cộng số trừ với số đối của số bị trừ |
| Nhân hai số nguyên cùng dấu | Nhân hai giá trị tuyệt đối và đặt dấu dương trước kết quả |
| Nhân hai số nguyên khác dấu | Nhân hai giá trị tuyệt đối và đặt dấu âm trước kết quả |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 60 SGK Toán 7 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!