Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 10 trang 12, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại \(x = - 5\). B. Hàm số có giá trị cực đại bằng 0. C. Hàm số đạt cực tiểu tại \(x = 2\). D. Hàm số đạt cực đại tại \(x = 4\).
Đề bài
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
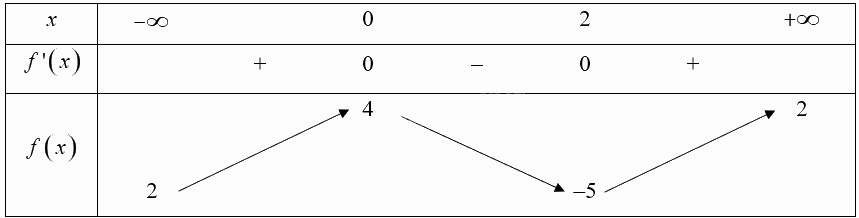
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại \(x = - 5\). B. Hàm số có giá trị cực đại bằng 0.
C. Hàm số đạt cực tiểu tại \(x = 2\). D. Hàm số đạt cực đại tại \(x = 4\).
Phương pháp giải - Xem chi tiết
Dựa vào bảng biến thiên để xác định các điểm cực trị.
Lời giải chi tiết
Dựa vào bảng biến thiên ta có:
+ Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\).
+ Hàm số có giá trị cực đại bằng 4.
Chọn C.
Bài 10 trang 12 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 10 trang 12 sách bài tập Toán 12 Cánh Diều, chúng ta cần phân tích đề bài một cách cẩn thận để xác định yêu cầu và các dữ kiện đã cho. Sau đó, áp dụng các kiến thức lý thuyết đã học để tìm ra lời giải chính xác.
Ví dụ (giả định bài 10 yêu cầu tính đạo hàm của hàm số y = x^3 - 2x^2 + 5x - 1):
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể luyện tập thêm với các bài tập tương tự trong sách bài tập Toán 12 Cánh Diều hoặc các nguồn tài liệu học tập khác.
Ngoài việc giải bài tập, bạn nên tìm hiểu thêm về các ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật. Điều này sẽ giúp bạn hiểu sâu hơn về tầm quan trọng của đạo hàm và mở rộng kiến thức của mình.
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = x^n | y' = nx^(n-1) |
| y = u + v | y' = u' + v' |
| y = u - v | y' = u' - v' |
Lưu ý: Đây chỉ là một ví dụ minh họa. Nội dung cụ thể của bài 10 trang 12 sách bài tập Toán 12 Cánh Diều có thể khác. Bạn cần xem lại đề bài gốc để giải quyết bài tập một cách chính xác.
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 10 trang 12 sách bài tập Toán 12 Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt!