Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 92 sách bài tập Toán 12 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán.
Một thư viện thống kê số người đến đọc sách vào buổi tối trong 30 ngày của một tháng và kết quả được cho bởi Bảng 11. a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó. b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Đề bài
Một thư viện thống kê số người đến đọc sách vào buổi tối trong 30 ngày của một tháng và kết quả được cho bởi Bảng 11.
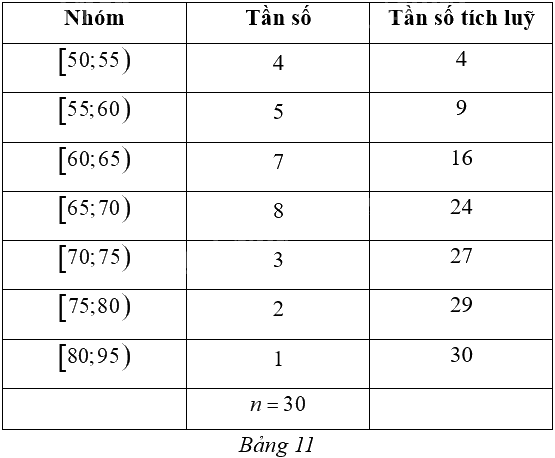
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p - 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\)). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p\), \(c{f_{p - 1}}\) là tần số tích luỹ của nhóm thứ \(p - 1\). Khi đó: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h\).
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q - 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\)). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\), \(c{f_{q - 1}}\) là tần số tích luỹ của nhóm thứ \(q - 1\). Khi đó: \({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
Lời giải chi tiết
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90 - 40 = 40\) (người).
b) Nhóm 2 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{30}}{4} = 7,5\).
Nhóm 2 có đầu mút trái \(s = 55\), độ dài \(h = 5\), tần số của nhóm \({n_2} = 5\) và nhóm 1 có tần số tích luỹ \(c{f_1} = 4\).
Ta có: \({Q_1} = s + \left( {\frac{{7,5 - c{f_1}}}{{{n_2}}}} \right).h = 55 + \left( {\frac{{7,5 - 4}}{5}} \right).5 = 58,5\).
Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.30}}{4} = 22,5\).
Nhóm 4 có đầu mút trái \(t = 65\), độ dài \(l = 5\), tần số của nhóm \({n_4} = 8\) và nhóm 3 có tần số tích luỹ \(c{f_3} = 16\).
Ta có: \({Q_3} = t + \left( {\frac{{22,5 - c{f_3}}}{{{n_4}}}} \right).l = 65 + \left( {\frac{{22,5 - 16}}{8}} \right).5 = 69,0625\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 69,0625 - 58,5 \approx 11\) (người).
Bài 8 trang 92 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế, đặc biệt là các bài toán liên quan đến tính đơn điệu của hàm số và tìm cực trị.
Bài 8 bao gồm các dạng bài tập sau:
Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm khoảng đồng biến, nghịch biến của hàm số.
Hướng dẫn giải:
Kết quả: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Tìm cực đại, cực tiểu của hàm số y = g(x) = x4 - 4x3 + 4x2 + 1.
Hướng dẫn giải:
Kết quả: Hàm số đạt cực đại tại x = 1 với giá trị là 2, đạt cực tiểu tại x = 0 và x = 2 với giá trị là 1.
Giaitoan.edu.vn cung cấp:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 8 trang 92 sách bài tập Toán 12 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!