Bài 9 trang 61 sách bài tập Toán 12 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 9 trang 61, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
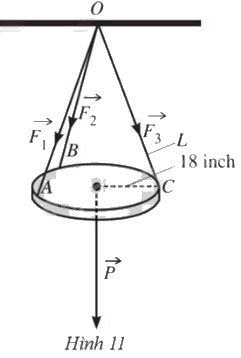
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \(O\) trên trần nhà lần lượt buộc vào ba điểm \(A,B,C\) trên đèn tròn (Hình 11). Độ dài của ba đoạn dây \(OA,OB,OC\) đều bằng \(L\left( {inch} \right)\). Trọng lượng của chiếc đèn là \(24N\) và bán kính của chiếc đèn là \(18inch\left( {1inch = 2,54cm} \right)\). Gọi \(F\) là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dâ
Đề bài
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \(O\) trên trần nhà lần lượt buộc vào ba điểm \(A,B,C\) trên đèn tròn (Hình 11). Độ dài của ba đoạn dây \(OA,OB,OC\) đều bằng \(L\left( {inch} \right)\). Trọng lượng của chiếc đèn là \(24N\) và bán kính của chiếc đèn là \(18inch\left( {1inch = 2,54cm} \right)\). Gọi \(F\) là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, \(F = F\left( L \right)\) là một hàm số với biến số là \(L\).
a) Xác định công thức tính hàm số \(F = F\left( L \right)\).
b) Khảo sát và vẽ đồ thị hàm số \(F = F\left( L \right)\).
c) Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là \(10N\).
Phương pháp giải - Xem chi tiết
Sơ đồ khảo sát hàm số:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
• Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm các đường tiệm cận của đồ thị (nếu có).
• Lập bảng biến thiên của hàm số, bao gồm: tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.
Bước 3. Vẽ đồ thị hàm số
• Vẽ các đường tiệm cận (nếu có).
• Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục toạ độ (trong trường hợp đơn giản),…
• Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Lời giải chi tiết
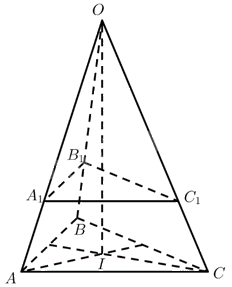
a) Gọi \({A_1},{B_1},{C_1}\)lần lượt là các điểm sao cho \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Khi đó, hai vectơ \(\overrightarrow {OA} ,\overrightarrow {O{A_1}} \) cùng phương, do đó tồn tại số \(k \ne 0\) sao cho: \(\overrightarrow {O{A_1}} = k.\overrightarrow {OA} \).
Tương tự ta có: \(\overrightarrow {O{B_1}} = k.\overrightarrow {OB} ,\overrightarrow {O{C_1}} = k.\overrightarrow {OC} \).
Suy ra, \(F = \left| {\overrightarrow {{F_1}} } \right| = k.\left| {\overrightarrow {OA} } \right| = k.L\) (1)
Do chiếc đèn ở vị trí cân bằng nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \).
Gọi \(I\) là tâm của chiếc đèn hình tròn.
Vì tam giác \(ABC\) là tam giác đều nên \(I\) cũng là trọng tâm của tam giác.
Sử dụng quy tắc trọng tâm trong tam giác \(ABC\), ta được:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OI} \Leftrightarrow \frac{1}{k}\left( {\overrightarrow {O{A_1}} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} } \right) = 3\overrightarrow {OI} \Leftrightarrow \frac{1}{k}.\overrightarrow P = 3\overrightarrow {OI} \Leftrightarrow \overrightarrow P = 3k.\overrightarrow {OI} \)
Theo giả thiết bài toán, trọng lượng của chiếc đèn là \(24N\), do đó \(OI = \frac{8}{k}\).
Mặt khác, xét hình chóp tam giác đều \(O.ABC\), có \(OI\) vuông góc mới mặt phẳng đáy \(\left( {ABC} \right)\). Khi đó: \(OI = \sqrt {O{A^2} - A{I^2}} = \sqrt {{L^2} - {{18}^2}} = \sqrt {{L^2} - 324} \).
Suy ra, \(\frac{8}{k} = \sqrt {{L^2} - 324} \Leftrightarrow k = \frac{8}{{\sqrt {{L^2} - 324} }}\) thế vào (1) ta được:
\(F = \frac{8}{{\sqrt {{L^2} - 324} }}.L \Leftrightarrow F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\left( N \right)\)
b) Ta khảo sát hàm số \(F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\) trên \(\left( {18; + \infty } \right)\).
1) Hàm số xác định trên \(\left( {18; + \infty } \right)\).
2) Sự biến thiên:
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } F = 8\).
Do đó, đường thẳng \(y = 8\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {{18}^ + }} F = + \infty \).
Do đó, đường thẳng \(x = 18\) là tiệm cận đứng của đồ thị hàm số.
• Bảng biến thiên:
\(F' = \frac{{{{\left( {8L} \right)}^\prime }.\sqrt {{L^2} - 324} - 8L.{{\left( {\sqrt {{L^2} - 324} } \right)}^\prime }}}{{{{\left( {\sqrt {{L^2} - 324} } \right)}^2}}} = \frac{{ - 2592}}{{\left( {{L^2} - 324} \right)\sqrt {{L^2} - 324} }} < 0,\forall x \in \left( {18; + \infty } \right)\).
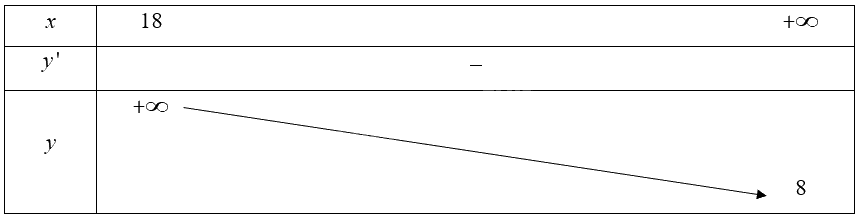
Hàm số nghịch biến trên \(\left( {18; + \infty } \right)\).
Hàm số không có cực trị trên \(\left( {18; + \infty } \right)\).
3) Đồ thị
Đồ thị hàm số không có giao điểm với trục tung.
Vậy đồ thị hàm số \(F=\frac{8L}{\sqrt{{{L}^{2}}-324}}\) trên \(\left( {18; + \infty } \right)\) như sau:
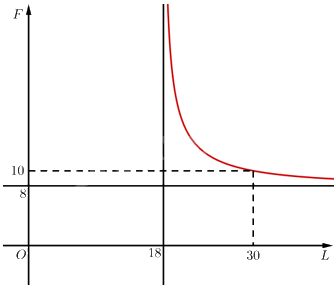
c) Khi lực căng của mỗi sợi dây bằng \(10N\), ta có:
\(\frac{8L}{\sqrt{{{L}^{2}}-324}}=10\Leftrightarrow 8L=10\sqrt{{{L}^{2}}-324}\Leftrightarrow 4L=5\sqrt{{{L}^{2}}-324}\)
\(\Leftrightarrow 16{{L}^{2}}=25\left( {{L}^{2}}-324 \right)\Leftrightarrow {{L}^{2}}=900\Leftrightarrow L=30\left( TMK \right)\)
Dựa vào đồ thị hàm số \(F = \frac{{8L}}{{\sqrt {{L^2} - 324} }}\) trên \(\left( {18; + \infty } \right)\) ở phần b), ta thấy chiều dài tối thiểu của mỗi sợi dây để lực căng tối đa là \(10N\) là \(30{\rm{ }}inch\).
Bài 9 trang 61 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh áp dụng các quy tắc đạo hàm cơ bản, đạo hàm của hàm hợp, và đạo hàm của hàm ẩn để giải quyết các bài toán liên quan đến việc tìm đạo hàm, khảo sát hàm số, và ứng dụng đạo hàm vào các bài toán thực tế.
Bài 9 thường bao gồm các dạng bài tập sau:
Bài toán: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số.
Lời giải:
Áp dụng quy tắc đạo hàm của hàm đa thức, ta có:
y' = 3x2 - 6x
Để giải bài tập đạo hàm hiệu quả, học sinh cần:
Khi giải bài tập đạo hàm, học sinh cần lưu ý:
Để học tốt môn Toán 12, học sinh có thể tham khảo các tài liệu sau:
Bài 9 trang 61 sách bài tập Toán 12 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc đạo hàm, luyện tập thường xuyên, và sử dụng các tài liệu tham khảo hữu ích, học sinh có thể tự tin giải quyết các bài tập đạo hàm một cách hiệu quả.