Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 45 trang 20, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 45 trang 20 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
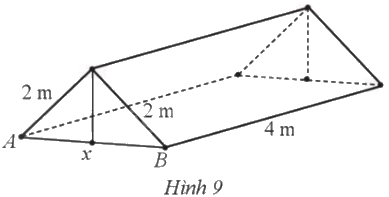
Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách \(AB\) để khoảng không gian trong lều là lớn nhất.
Đề bài
Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách \(AB\) để khoảng không gian trong lều là lớn nhất.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích hình lăng trụ để tính thể tích \(V\left( x \right)\) của không gian trong lều, sau đó tìm giá trị lớn nhất của hàm số \(V\left( x \right)\).
Lời giải chi tiết
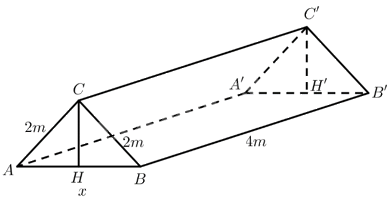
Giả sử lều dựng lên được hình lăng trụ đứng \(ABC.A'B'C'\) với \(AC = BC = 2,BB' = 4,\)\(AB = x\left( {0 < x < 4} \right)\).
\(AH = \frac{x}{2} \Rightarrow CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {4 - \frac{{{x^2}}}{4}} \)
\({S_{\Delta ABC}} = AB.CH = x.\sqrt {4 - \frac{{{x^2}}}{4}} \)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.BB' = x.\sqrt {4 - \frac{{{x^2}}}{4}} .4 = 2x\sqrt {16 - {x^2}} \).
Xét hàm số \(V\left( x \right) = 2x\sqrt {16 - {x^2}} \) trên khoảng \(\left( {0;4} \right)\)
Ta có: \(y' = {\left( {2x} \right)^\prime }\sqrt {16 - {x^2}} + 2x.{\left( {\sqrt {16 - {x^2}} } \right)^\prime } = 2\sqrt {16 - {x^2}} + 2x.\frac{{ - x}}{{\sqrt {16 - {x^2}} }} = \frac{{2\left( {8 - {x^2}} \right)}}{{\sqrt {16 - {x^2}} }}\)
\(y' = 0\) khi \(x = 2\sqrt 2 \).
Bảng biến thiên của hàm số:
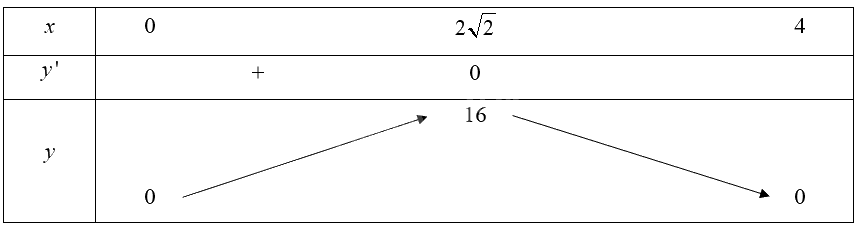
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left( {0;4} \right)} V\left( x \right) = 16\) tại \({\rm{x}} = 2\sqrt 2 \).
Vậy \(AB = 2\sqrt 2 \) thì khoảng không gian trong lều là lớn nhất.
Bài 45 trang 20 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của bài 45 trang 20 sách bài tập Toán 12 Cánh Diều:
(Giả sử đề bài là: Tính đạo hàm của các hàm số sau: a) y = sin(2x + 1); b) y = cos(x^2); c) y = tan(3x - 2))
Để tính đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Vậy, đạo hàm của hàm số y = sin(2x + 1) là y' = 2cos(2x + 1).
Tương tự như bài 45a, ta áp dụng quy tắc đạo hàm hàm hợp để tính đạo hàm của hàm số y = cos(x^2).
Vậy, đạo hàm của hàm số y = cos(x^2) là y' = -2xsin(x^2).
Để tính đạo hàm của hàm số y = tan(3x - 2), ta sử dụng quy tắc đạo hàm của hàm tan và quy tắc đạo hàm hàm hợp.
Vậy, đạo hàm của hàm số y = tan(3x - 2) là y' = 3sec^2(3x - 2).
Qua việc giải chi tiết bài 45 trang 20 sách bài tập Toán 12 Cánh Diều, chúng ta đã củng cố kiến thức về quy tắc đạo hàm của hàm hợp và đạo hàm của các hàm lượng giác. Để nắm vững kiến thức này, bạn nên:
Giaitoan.edu.vn hy vọng bài viết này đã giúp bạn giải quyết bài toán một cách hiệu quả. Chúc bạn học tập tốt!