Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 15 trang 13 Sách bài tập Toán 12 - Cánh Diều. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
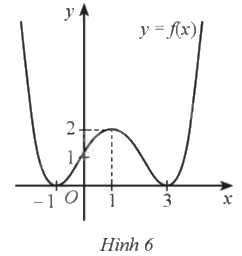
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là: A. 2. B. 1. C. ‒1. D. 0.
Đề bài
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là:
A. 2.
B. 1.
C. ‒1.
D. 0.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số xác định các cực trị của hàm số.
Lời giải chi tiết
Dựa vào đồ thị ta có: Hàm số đạt cực tiểu tại \(x = - 1\) và \(x = 3\). Khi đó giá trị cực tiểu bằng 0.
Chọn D.
Bài 15 trang 13 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, hàm ẩn và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Bài 15 bao gồm một loạt các bài tập khác nhau, từ việc tính đạo hàm của các hàm số đơn giản đến việc giải các bài toán liên quan đến tiếp tuyến của đường cong, cực trị của hàm số và ứng dụng đạo hàm trong các bài toán thực tế.
Các câu hỏi trong phần này thường yêu cầu học sinh tính đạo hàm của các hàm số đa thức, phân thức, lượng giác và hàm mũ. Để giải quyết các bài toán này, học sinh cần nắm vững các công thức đạo hàm cơ bản và quy tắc tính đạo hàm.
Để tìm tiếp tuyến của đường cong tại một điểm cho trước, học sinh cần xác định hệ số góc của tiếp tuyến bằng cách tính đạo hàm của hàm số tại điểm đó. Sau đó, sử dụng phương trình đường thẳng đi qua một điểm với hệ số góc đã biết để viết phương trình tiếp tuyến.
Để tìm cực trị của hàm số, học sinh cần tìm các điểm mà đạo hàm của hàm số bằng 0 hoặc không tồn tại. Sau đó, sử dụng tiêu chuẩn xét dấu đạo hàm để xác định xem các điểm đó là điểm cực đại hay cực tiểu.
Để giải bài tập trong bài 15 trang 13 Sách bài tập Toán 12 - Cánh Diều một cách hiệu quả, học sinh nên:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + 2(x2)' - 5(x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Trong quá trình giải bài tập, học sinh cần lưu ý:
Bài 15 trang 13 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, các bạn học sinh sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.