Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 48 trang 27 Sách bài tập Toán 12 - Cánh Diều. Bài viết này cung cấp đáp án, phương pháp giải và giải thích rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S). Cho hình phẳng được tô màu như Hình 12. Diện tích hình phẳng được kí hiệu là (S). a) Hình phẳng đó được giới hạn bởi đồ thị (y = fleft( x right)), trục hoành và hai đường thẳng (x = - 1,x = 5). b) (S = intlimits_{ - 1}^5 {left| {fleft( x right)} right|dx} ). c) (S = intlimits_{ - 1}^1 {fleft( x right)dx} + intlimits_1^5 {fleft( x right)dx} ). d) (S = intlimits_{ - 1}^1 {fleft( x right)dx} -
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
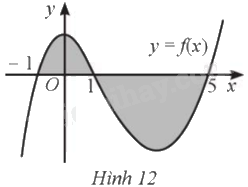
Cho hình phẳng được tô màu như Hình 12. Diện tích hình phẳng được kí hiệu là \(S\).
a) Hình phẳng đó được giới hạn bởi đồ thị \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 1,x = 5\).
b) \(S = \int\limits_{ - 1}^5 {\left| {f\left( x \right)} \right|dx} \).
c) \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^5 {f\left( x \right)dx} \).
d) \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^5 {f\left( x \right)dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
Hình phẳng đã cho được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 1,x = 5\). Vậy a) đúng.
Diện tích hình phẳng được tính theo công thức:
\(S = \int\limits_{ - 1}^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^5 {f\left( x \right)dx} \) (vì \(f\left( x \right) > 0,\forall x \in \left[ { - 1;1} \right]\) và \(f\left( x \right) < 0,\forall x \in \left[ {1;5} \right]\)).
Vậy b) đúng, c) sai, d) đúng.
a) Đ.
b) Đ.
c) S.
d) Đ.
Bài 48 trang 27 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết.
Để giải quyết bài 48 trang 27 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài 48 thường được chia thành nhiều phần nhỏ, mỗi phần yêu cầu học sinh giải quyết một dạng bài tập cụ thể. Dưới đây là hướng dẫn giải chi tiết từng phần:
Để giải các bài tập về hàm số, học sinh cần:
Khi giải các bài tập về đạo hàm, học sinh cần:
Để giải các bài tập về tích phân, học sinh cần:
Khi giải các bài tập về số phức, học sinh cần:
Để đạt được kết quả tốt nhất khi giải bài 48 trang 27, học sinh cần lưu ý những điều sau:
Bài 48 trang 27 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ giải quyết bài tập một cách hiệu quả và đạt được kết quả tốt nhất.