Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 91 sách bài tập Toán 12 - Cánh diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9. a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: (R = 90) (tuổi). b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng (frac{n}{4} = frac{{200}}{4} = 50). c) ({Q_3} = 52frac{{17}}{{24}}). d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20. A. 120. B. 80. C. 20. D. 200.
Đề bài
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9.
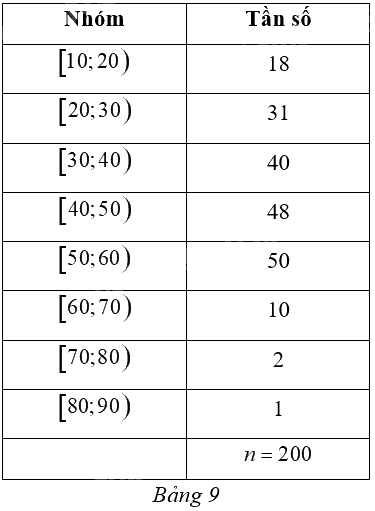
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90\) (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{200}}{4} = 50\).
c) \({Q_3} = 52\frac{{17}}{{24}}\).
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p - 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\)). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p\), \(c{f_{p - 1}}\) là tần số tích luỹ của nhóm thứ \(p - 1\). Khi đó: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h\).
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q - 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\)). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\), \(c{f_{q - 1}}\) là tần số tích luỹ của nhóm thứ \(q - 1\). Khi đó: \({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
Lời giải chi tiết
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90 - 10 = 80\). Vậy a) sai.
Ta có bảng sau:
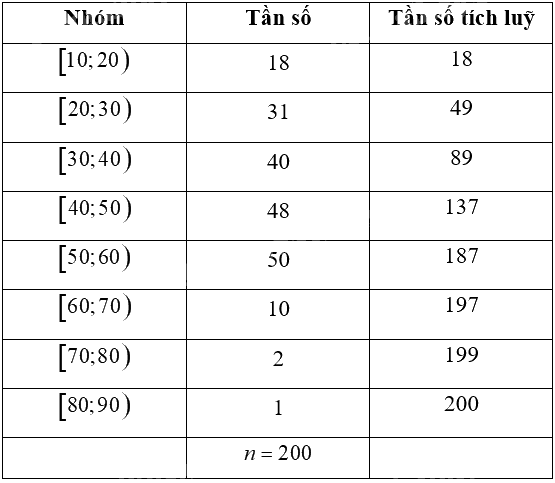
Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{200}}{4} = 50\). Vậy b) đúng.
Nhóm 3 có đầu mút trái \(s = 30\), độ dài \(h = 10\), tần số của nhóm \({n_3} = 40\) và nhóm 2 có tần số tích luỹ \(c{f_2} = 49\).
Ta có: \({Q_1} = s + \left( {\frac{{50 - c{f_2}}}{{{n_3}}}} \right).h = 30 + \left( {\frac{{50 - 49}}{{40}}} \right).10 = 30,25\) (tuổi).
Nhóm 5 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.200}}{4} = 150\).
Nhóm 5 có đầu mút trái \(t = 50\), độ dài \(l = 10\), tần số của nhóm \({n_5} = 50\) và nhóm 4 có tần số tích luỹ \(c{f_4} = 137\).
Ta có: \({Q_3} = t + \left( {\frac{{150 - c{f_4}}}{{{n_5}}}} \right).l = 50 + \left( {\frac{{150 - 137}}{{50}}} \right).10 = 52,6\) (tuổi). Vậy c) sai.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 52,6 - 30,25 = 22,35 > 20\). Vậy d) đúng.
a) S.
b) Đ.
c) S.
d) Đ.
Bài 6 trang 91 sách bài tập Toán 12 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số lượng giác, hàm hợp và các hàm số đặc biệt khác. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, không chỉ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các môn học nâng cao ở bậc đại học.
Bài 6 trang 91 sách bài tập Toán 12 - Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng câu hỏi trong bài 6 trang 91 sách bài tập Toán 12 - Cánh diều. (Ở đây sẽ là nội dung giải chi tiết từng câu, ví dụ)
Để tính đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Trong trường hợp này, u(t) = sin(t) và v(x) = 2x + 1.
Ta có: u'(t) = cos(t) và v'(x) = 2.
Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1).
Tương tự như ví dụ trên, ta sử dụng quy tắc đạo hàm của hàm hợp.
Trong trường hợp này, u(t) = e^t và v(x) = x^2.
Ta có: u'(t) = e^t và v'(x) = 2x.
Vậy, y' = e^(x^2) * 2x = 2xe^(x^2).
Để giải nhanh các bài tập về đạo hàm, các em cần:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 6 trang 91 sách bài tập Toán 12 - Cánh diều là một bài tập quan trọng giúp các em rèn luyện kỹ năng tính đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
| y = e^x | y' = e^x |