Bài 96 trang 41 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 12, thường tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải toán để có thể hoàn thành một cách chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 96 trang 41 Sách bài tập Toán 12 - Cánh Diều, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn trong các bài kiểm tra.
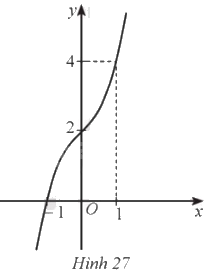
Đường cong ở Hình 27 là đồ thị của hàm số: A. \(y = 2{{\rm{x}}^3} + 2\). B. \(y = {x^3} - {x^2} + 2\). C. \(y = - {x^3} + 3{\rm{x}} + 2\). D. \(y = {x^3} + x + 2\).
Đề bài
Đường cong ở Hình 27 là đồ thị của hàm số:
A. \(y = 2{{\rm{x}}^3} + 2\).
B. \(y = {x^3} - {x^2} + 2\).
C. \(y = - {x^3} + 3{\rm{x}} + 2\).
D. \(y = {x^3} + x + 2\).
Phương pháp giải - Xem chi tiết
‒ Dựa vào hình dáng của đồ thị hàm số.
‒ Xét các điểm trên đồ thị hàm số.
Lời giải chi tiết
Dựa vào hình dáng của đồ thị hàm số ta có: \(a > 0\) và \(y' > 0\) nên loại A, C.
Đồ thị hàm số đi qua điểm \(\left( { - 1;0} \right)\) nên loại B.
Chọn D.
Bài 96 trang 41 Sách bài tập Toán 12 - Cánh Diều thường xoay quanh việc khảo sát hàm số bậc ba bằng phương pháp đạo hàm. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử hàm số cần khảo sát là:
f(x) = x3 - 3x2 + 2
Hàm số f(x) = x3 - 3x2 + 2 xác định trên tập số thực R.
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0, ta được:
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm cực trị.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Từ bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
f''(x) = 6x - 6
Giải phương trình f''(x) = 0, ta được:
6x - 6 = 0 ⇔ x = 1
Vậy, x = 1 là điểm uốn.
Hàm số f(x) = x3 - 3x2 + 2 không có tiệm cận.
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số f(x) = x3 - 3x2 + 2.
Giaitoan.edu.vn là địa chỉ tin cậy cho các em học sinh cần tìm kiếm lời giải bài tập Toán, đặc biệt là các bài tập khó và phức tạp. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong học tập. Hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất!