Giải bài 1 trang 60 Sách bài tập Toán 12 - Cánh Diều

Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều

Giải bài 1 trang 60 Sách bài tập Toán 12 - Cánh Diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 60 sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.

Cho tứ diện (ABCD). Lấy (G) là trọng tâm tam giác (BCD). Phát biểu nào sau đây là sai? A. (overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). B. (overrightarrow {GA} + overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). C. (overrightarrow {CB} + overrightarrow {CD} = 3overrightarrow {CG} ). D. (overrightarrow {AB} + overrightarrow {AC} + overrightarrow {AD} = 3overrightarrow {AG} ).

Đề bài

Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai?

A. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)

B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)

C. \(\overrightarrow {CB} + \overrightarrow {CD} = 3\overrightarrow {CG} \)

D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).

Phương pháp giải - Xem chi tiết Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều 1

‒ Sử dụng tính chất trung điểm của đoạn thẳng và tính chất trọng tâm của tam giác.

Lời giải chi tiết

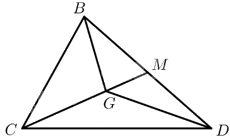
Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều 2

Theo tính chất trọng tâm của tam giác, với \(G\) là trọng tâm tam giác \(BCD\), ta có: \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Vậy A đúng.

Gọi \(M\) là trung điểm của \(BD\). Ta có:

\(\overrightarrow {CB} + \overrightarrow {CD} = 2\overrightarrow {CM} = 2.\frac{2}{3}\overrightarrow {CG} = 3\overrightarrow {CG} \). Vậy C đúng.

Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {AG} + \overrightarrow {GC} + \overrightarrow {AG} + \overrightarrow {GD} = 3\overrightarrow {AG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 3\overrightarrow {AG} \). Vậy D đúng.

Chọn B.

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều đặc sắc thuộc chuyên mục đề toán lớp 12 trên nền tảng toán math. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 1 trang 60 Sách bài tập Toán 12 - Cánh Diều: Tổng quan

Bài 1 trang 60 sách bài tập Toán 12 - Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm.

Nội dung bài tập

Bài 1 trang 60 sách bài tập Toán 12 - Cánh Diều thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số tại một điểm.
Tìm đạo hàm của hàm số.
Vận dụng đạo hàm để giải các bài toán liên quan đến tốc độ thay đổi, cực trị của hàm số.

Lời giải chi tiết bài 1 trang 60

Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, đây chỉ là một trong nhiều cách giải bài tập, bạn có thể tìm tòi và khám phá các phương pháp giải khác nhau để nâng cao khả năng giải toán của mình.

Phần 1: Tính đạo hàm của hàm số tại một điểm

Để tính đạo hàm của hàm số tại một điểm, bạn có thể sử dụng định nghĩa đạo hàm hoặc các quy tắc tính đạo hàm đã học. Ví dụ, nếu hàm số là f(x) = x², thì đạo hàm của hàm số tại điểm x = 2 là f'(2) = 2x|_x=2 = 4.

Phần 2: Tìm đạo hàm của hàm số

Để tìm đạo hàm của hàm số, bạn cần áp dụng các quy tắc tính đạo hàm cho từng thành phần của hàm số. Ví dụ, nếu hàm số là f(x) = x³ + 2x² - 5x + 1, thì đạo hàm của hàm số là f'(x) = 3x² + 4x - 5.

Phần 3: Vận dụng đạo hàm để giải các bài toán thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như tính tốc độ thay đổi của một đại lượng, tìm cực trị của hàm số, hoặc giải các bài toán tối ưu hóa. Để giải các bài toán này, bạn cần hiểu rõ ý nghĩa của đạo hàm và cách vận dụng đạo hàm vào từng bài toán cụ thể.

Ví dụ minh họa

Giả sử, chúng ta có bài toán sau:

Cho hàm số f(x) = x² - 4x + 3. Tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm của hàm số: f'(x) = 2x - 4.
Tìm các điểm mà đạo hàm bằng 0: 2x - 4 = 0 => x = 2.
Xác định loại cực trị:

Nếu f''(x) > 0 thì x là điểm cực tiểu.
Nếu f''(x) < 0 thì x là điểm cực đại.

Tính đạo hàm bậc hai: f''(x) = 2.
Vì f''(2) = 2 > 0, nên x = 2 là điểm cực tiểu.
Giá trị cực tiểu của hàm số là f(2) = 2² - 4*2 + 3 = -1.

Lưu ý khi giải bài tập

Khi giải bài tập về đạo hàm, bạn cần lưu ý những điều sau:

Nắm vững các khái niệm cơ bản về đạo hàm.
Hiểu rõ các quy tắc tính đạo hàm.
Vận dụng đạo hàm một cách linh hoạt vào từng bài toán cụ thể.
Kiểm tra lại kết quả sau khi giải bài tập.

Tổng kết

Bài 1 trang 60 sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng rằng, với lời giải chi tiết và những lưu ý trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!