Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 46 trang 26 Sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho các hàm số (y = fleft( x right),y = gleft( x right)) có đồ thị lần lượt là (left( P right),left( C right)) và hình phẳng được tô màu như Hình 11. Công thức tính diện tích hình phẳng được tô màu là: A. (S = intlimits_{ - 1}^1 {left[ {gleft( x right) - fleft( x right)} right]dx} + intlimits_1^2 {left[ {gleft( x right) - fleft( x right)} right]dx} ). B. (S = intlimits_{ - 1}^1 {left[ {gleft( x right) - fleft( x right)} right]dx} - intlimits_1^2 {lef
Đề bài
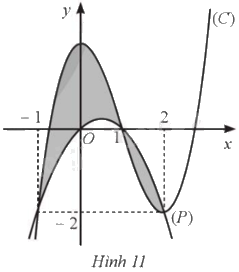
Cho các hàm số \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị lần lượt là \(\left( P \right),\left( C \right)\) và hình phẳng được tô màu như Hình 11. Công thức tính diện tích hình phẳng được tô màu là:
A. \(S = \int\limits_{ - 1}^1 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} + \int\limits_1^2 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \).
B. \(S = \int\limits_{ - 1}^1 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} - \int\limits_1^2 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \).
C. \(S = \int\limits_{ - 1}^2 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \).
D. \(S = \int\limits_{ - 1}^2 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
Diện tích hình phẳng được tính theo công thức:
\(\begin{array}{l}S = \int\limits_{ - 1}^2 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_{ - 1}^1 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} + \int\limits_1^2 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \\ = \int\limits_{ - 1}^1 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} - \int\limits_1^2 {\left[ {g\left( x \right) - f\left( x \right)} \right]dx} \end{array}\)
(vì \(g\left( x \right) > f\left( x \right),\forall x \in \left[ { - 1;1} \right]\) và \(f\left( x \right) > g\left( x \right),\forall x \in \left[ {1;2} \right]\)).
Chọn B.
Bài 46 trang 26 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 46 trang 26, yêu cầu thường là tìm đạo hàm của hàm số, giải phương trình đạo hàm bằng 0 để tìm điểm cực trị, và xác định khoảng đơn điệu của hàm số dựa trên dấu của đạo hàm.
Để giải bài tập về đạo hàm một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng ý của bài 46, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Giả sử bài 46 yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x. Ta thực hiện như sau:
Khi giải bài tập về đạo hàm, bạn cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 46 trang 26 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết và dễ hiểu này, bạn sẽ có thể giải bài tập một cách nhanh chóng và hiệu quả. Chúc bạn học tốt!