Chào mừng các em học sinh đến với lời giải chi tiết bài 55 trang 24 Sách bài tập Toán 12 - Cánh Diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hàm số (y = fleft( x right)) xác định trên (mathbb{R}backslash left{ { - 2} right}), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Khẳng định nào sau đây là đúng? A. Đồ thị hàm số có tiệm cận đứng là đường thẳng (x = - 2) và không có tiệm cận ngang. B. Đồ thị hàm số có tiệm cận đứng là đường thẳng (x = - 2) và tiệm cận ngang là đường thẳng (y = 3). C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng (y = - 2). D. Đồ thị hàm
Đề bài
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
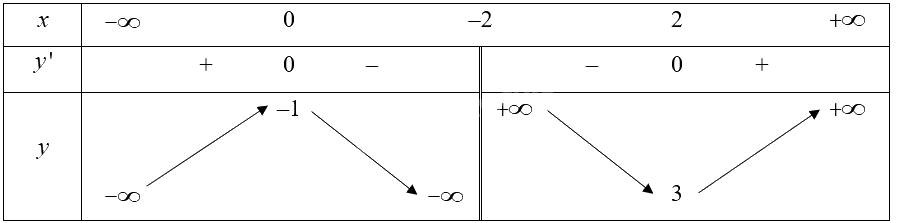
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và không có tiệm cận ngang.
B. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).
C. Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang là đường thẳng \(y = - 2\).
D. Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 2\) và tiệm cận ngang là đường thẳng \(y = 3\).
Phương pháp giải - Xem chi tiết
‒ Tìm tiệm cận đứng: Tính \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right)\), nếu một trong các giới hạn sau thoả mãn: \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \)
thì đường thẳng \(x = {x_0}\) là đường tiệm cận đứng.
‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.
Lời giải chi tiết
Dựa vào bảng biến thiên ta có:
• \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = - \infty \).
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số đã cho.
• \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \).
Vậy hàm số không có tiệm cận ngang.
Chọn A.
Bài 55 trang 24 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường yêu cầu học sinh vận dụng các công thức, định lý và kỹ năng giải toán đã được trang bị để giải quyết các bài toán cụ thể.
Bài 55 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh giải quyết bài tập một cách hiệu quả, giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng câu hỏi trong bài 55 trang 24 Sách bài tập Toán 12 - Cánh Diều.
Đề bài: Giải phương trình lượng giác: sin(x) = 1/2
Lời giải:
Đề bài: Tính đạo hàm của hàm số: f(x) = x2 + 2x - 1
Lời giải:
f'(x) = 2x + 2
Giải thích chi tiết quy tắc tính đạo hàm và áp dụng vào hàm số đã cho.
Để đạt kết quả tốt trong môn Toán 12, các em học sinh cần:
Hy vọng rằng lời giải chi tiết bài 55 trang 24 Sách bài tập Toán 12 - Cánh Diều sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải toán. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán 12!
| Chủ đề | Nội dung |
|---|---|
| Phương trình lượng giác | Giải phương trình sin(x) = 1/2 |
| Đạo hàm | Tính đạo hàm của hàm số f(x) = x2 + 2x - 1 |