Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 79 trang 38 sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
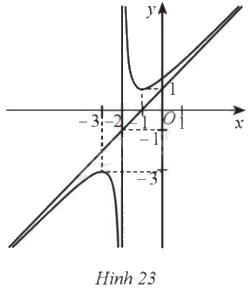
Cho hàm số (y = fleft( x right) = frac{{a{x^2} + bx + c}}{{mx + n}}) (với (a,m ne 0)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số: a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số. b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số. c) Phương trình (fleft( x right) = 3) có bao nhiêu nghiệm? d) Tìm công thức xác định hàm số (y = fleft( x right)), biết (m = 1).
Đề bài
Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a,m \ne 0\)) có đồ thị là đường cong như Hình 23. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.
c) Phương trình \(f\left( x \right) = 3\) có bao nhiêu nghiệm?
d) Tìm công thức xác định hàm số \(y = f\left( x \right)\), biết \(m = 1\).
Phương pháp giải - Xem chi tiết
‒ Xét đồ thị hàm số.
‒ Xét các đường tiệm cận của đồ thị hàm số.
‒ Xét các điểm trên đồ thị hàm số.
Lời giải chi tiết
a) Dựa vào đồ thị hàm số, ta có:
‒ Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 1; + \infty } \right)\); nghịch biến trên các khoảng \(\left( { - 3; - 2} \right)\) và \(\left( { - 2; - 1} \right)\).
‒ Hàm số đạt cực đại tại điểm \(x = - 3\), đạt cực tiểu tại điểm \(x = - 1\).
b)
• Tiệm cận đứng của đồ thị hàm số đi qua điểm có hoành độ ‒2.
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
• Tiệm cận xiên của đồ thị hàm số đi qua hai điểm \(\left( { - 1;0} \right)\) và \(\left( { - 2; - 1} \right)\).
Vậy đường thẳng \(y = x + 1\) là tiệm cận xiên của đồ thị hàm số.
c) Đường thẳng \(y = 3\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm. Vậy phương trình \(f\left( x \right) = 3\) có 2 nghiệm.
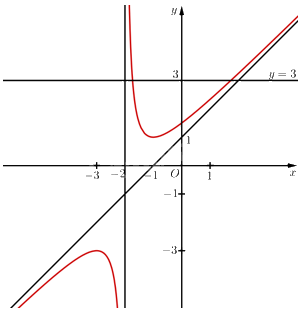
d) Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng. Vậy \( - \frac{n}{m} = - 2 \Leftrightarrow - \frac{n}{1} = - 2 \Leftrightarrow n = 2\).
Tiệm cận xiên của đồ thị hàm số có hệ số góc bằng 1. Vậy \(\frac{a}{m} = 1 \Leftrightarrow \frac{a}{1} = 1 \Leftrightarrow a = 1\).
Đồ thị hàm số đi qua điểm \(\left( { - 1;1} \right)\) nên ta có: \(\frac{{1.{{\left( { - 1} \right)}^2} + b.\left( { - 1} \right) + c}}{{\left( { - 1} \right) + 2}} = 1 \Leftrightarrow - b + c = 0\).
Đồ thị hàm số đi qua điểm \(\left( { - 3; - 3} \right)\) nên ta có: \(\frac{{1.{{\left( { - 3} \right)}^2} + b.\left( { - 3} \right) + c}}{{\left( { - 3} \right) + 2}} = - 3 \Leftrightarrow - 3b + c = - 6\).
Từ đó ta có \(b = 3,c = 3\).
Vậy hàm số cần tìm là: \(y = f\left( x \right) = \frac{{{x^2} + 3{\rm{x}} + 3}}{{{\rm{x}} + 2}}\).
Bài 79 trang 38 sách bài tập Toán 12 - Cánh Diều thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị, khoảng đơn điệu và vẽ đồ thị hàm số. Việc nắm vững các khái niệm và kỹ năng này là rất quan trọng để đạt kết quả tốt trong các kỳ thi Toán.
Bài 79 thường bao gồm các dạng bài tập sau:
Để giải bài 79 trang 38 sách bài tập Toán 12 - Cánh Diều một cách hiệu quả, bạn cần thực hiện các bước sau:
Ví dụ: Xét hàm số y = x3 - 3x2 + 2. Hãy tìm cực trị và khoảng đơn điệu của hàm số.
Giải:
Kết luận: Hàm số đạt cực đại tại x = 0 với giá trị y = 2 và đạt cực tiểu tại x = 2 với giá trị y = -2.
Để giải bài 79 trang 38 sách bài tập Toán 12 - Cánh Diều một cách chính xác, bạn cần lưu ý những điều sau:
Để hỗ trợ bạn trong quá trình học tập và giải bài tập Toán 12, chúng tôi xin giới thiệu một số tài liệu tham khảo hữu ích:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 79 trang 38 sách bài tập Toán 12 - Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi Toán!