Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 27 trang 17 Sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Giá trị lớn nhất của hàm số (y = frac{{2{rm{x}} - 1}}{{x - 2}}) trên nửa khoảng (left[ { - 3;2} right)) bằng: A. ( - frac{7}{5}). B. 7. C. (frac{7}{5}). D. ‒7.
Đề bài
Giá trị lớn nhất của hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x - 2}}\) trên nửa khoảng \(\left[ { - 3;2} \right)\) bằng:
A. \( - \frac{7}{5}\).
B. 7.
C. \(\frac{7}{5}\).
D. ‒7.
Phương pháp giải - Xem chi tiết
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Xét hàm số \(y = \frac{{2{\rm{x}} - 1}}{{x - 2}}\) trên nửa khoảng \(\left[ { - 3;2} \right)\).
Ta có:
\({y^\prime } = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \ne 2\)
Bảng biến thiên của hàm số:
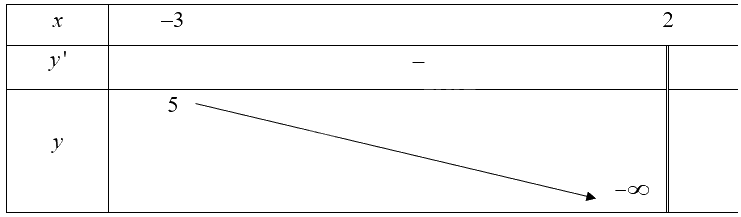
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left[ { - 3;2} \right)} f\left( x \right) = \frac{7}{5}\) tại \({\rm{x}} = - 3\).
Chọn C.
Bài 27 trang 17 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các khái niệm và công thức liên quan.
Trước khi đi vào giải bài tập cụ thể, chúng ta hãy cùng nhau ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 27 trang 17, chúng ta cần phân tích đề bài và xác định phương pháp giải phù hợp. Thông thường, bài tập này sẽ yêu cầu bạn thực hiện một trong các thao tác sau:
Ví dụ minh họa: (Giả sử bài 27 yêu cầu tìm cực trị của hàm số y = x^3 - 3x^2 + 2)
Bước 1: Tính đạo hàm cấp 1: y' = 3x^2 - 6x
Bước 2: Tìm các điểm cực trị: Giải phương trình y' = 0 => 3x^2 - 6x = 0 => x = 0 hoặc x = 2
Bước 3: Xác định loại cực trị:
Vậy, hàm số đạt cực đại tại x = 0, giá trị cực đại là y(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là y(2) = -2.
Để nắm vững kiến thức và kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Dưới đây là một số bài tập gợi ý:
Ngoài việc giải các bài tập trong sách bài tập, bạn có thể tìm hiểu thêm về các ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật,... Điều này sẽ giúp bạn hiểu sâu hơn về tầm quan trọng của đạo hàm trong cuộc sống.
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = x^n | y' = nx^(n-1) |
| y = u + v | y' = u' + v' |
| y = u.v | y' = u'v + uv' |
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài 27 trang 17 Sách bài tập Toán 12 - Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!