Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Giá trị nhỏ nhất của hàm số (y = sqrt {{x^2} + 4} ) bằng: A. 2. B. 4. C. 0. D. 1.
Đề bài
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 4} \) bằng:
A. 2.
B. 4.
C. 0.
D. 1.
Phương pháp giải - Xem chi tiết
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = \frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} = \frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} = \frac{{\rm{x}}}{{\sqrt {{x^2} + 4} }}\)
\(y' = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
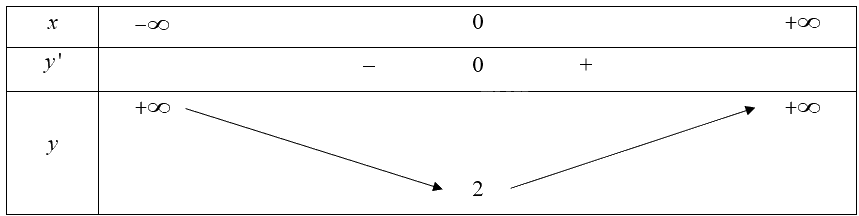
Căn cứ vào bảng biến thiên, ta có: \(\min f\left( x \right) = 2\) tại \({\rm{x}} = 0\).
Chọn A.
Bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết.
Bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều, chúng tôi xin trình bày lời giải chi tiết cho từng bài tập:
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài 1, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài 2, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài 3, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Để giải tốt các bài tập trong bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều, học sinh cần nắm vững các phương pháp sau:
Khi giải bài tập trong bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều, học sinh cần lưu ý những điều sau:
Bài 26 trang 17 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và phương pháp giải mà chúng tôi cung cấp, các bạn học sinh sẽ tự tin hơn khi giải bài tập này.
| Dạng bài | Phương pháp giải |
|---|---|
| Đạo hàm | Tính đạo hàm, giải phương trình đạo hàm |
| Khảo sát hàm số | Xác định cực trị, khoảng đơn điệu |