Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 23 trang 96 sách bài tập Toán 12 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán.
Giả sử trong một nhóm 80 người có 69 người không nhiễm bệnh và 11 người nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,9; còn đối với người không nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,05. a) Vẽ sơ đồ hình cây biểu thị tình huống trên. b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là ngư
Đề bài
Giả sử trong một nhóm 80 người có 69 người không nhiễm bệnh và 11 người nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,9; còn đối với người không nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,05.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Phương pháp giải - Xem chi tiết
‒ Sử dụng sơ đồ hình cây.
‒ Sử dụng công thức tính xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
‒ Sử dụng công thức Bayes: \(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}}\).
Lời giải chi tiết
a) Xét các biến cố:
\(A\): “Người được chọn nhiễm bệnh”;
\(B\): “Người được chọn xét nghiệm có kết quả dương tính”;
Trong một nhóm 80 người có 69 người không nhiễm bệnh và 11 người nhiễm bệnh nên ta có \(P\left( A \right) = \frac{{11}}{{80}};P\left( {\overline A } \right) = \frac{{69}}{{80}}\).
Đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,9 nên ta có \(P\left( {B|A} \right) = 0,9\).
Đối với người không nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,05 nên ta có \(P\left( {B|\overline A } \right) = 0,05\).
Ta có sơ đồ hình cây như sau:
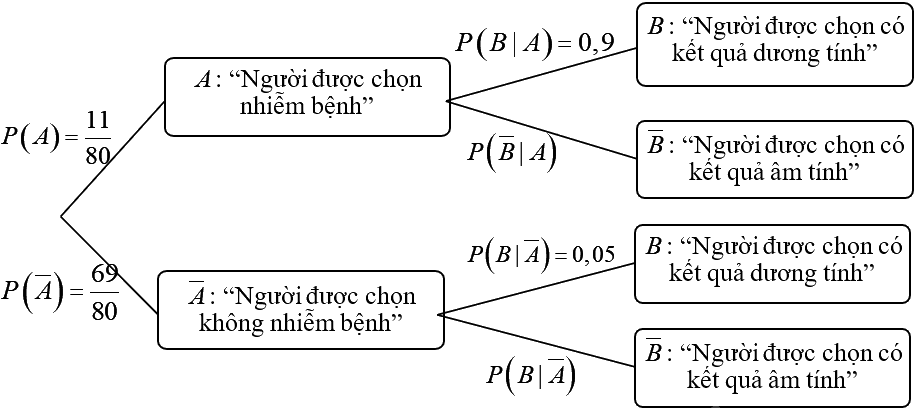
b) Xác suất để X xét nghiệm có kết quả dương tính là:
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = \frac{{11}}{{80}}.0,9 + \frac{{69}}{{80}}.0,05 = \frac{{267}}{{1600}}\).
Xác suất để X là người nhiễm bệnh là:
\(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{\frac{{11}}{{80}}.0,9}}{{\frac{{267}}{{1600}}}} = \frac{{66}}{{89}}\).
Bài 23 trang 96 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản, kết hợp với các kỹ năng biến đổi đại số để tìm đạo hàm của hàm số phức tạp hơn.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của bài 23 trang 96 sách bài tập Toán 12 Cánh Diều:
(Giả sử đề bài là: Tính đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1)
Để giải bài toán này, chúng ta sẽ sử dụng các quy tắc tính đạo hàm sau:
Áp dụng các quy tắc trên, ta có:
f'(x) = (x^3)' - 2(x^2)' + 5(x)' - (1)'
f'(x) = 3x^2 - 2(2x) + 5(1) - 0
f'(x) = 3x^2 - 4x + 5
Vậy, đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1 là f'(x) = 3x^2 - 4x + 5.
Để hiểu rõ hơn về cách tính đạo hàm, chúng ta cùng xem xét một số ví dụ minh họa khác:
Ví dụ 1: Tính đạo hàm của hàm số g(x) = 2x^4 + x - 7
Lời giải: g'(x) = 8x^3 + 1
Ví dụ 2: Tính đạo hàm của hàm số h(x) = -x^2 + 3x + 2
Lời giải: h'(x) = -2x + 3
Ngoài ra, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 12 Cánh Diều để rèn luyện kỹ năng.
Khi tính đạo hàm, bạn cần lưu ý một số điểm sau:
Để hiểu sâu hơn về đạo hàm, bạn có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như:
Bài 23 trang 96 sách bài tập Toán 12 Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng tính đạo hàm. Hy vọng rằng, với hướng dẫn chi tiết này, bạn đã nắm vững kiến thức và tự tin hơn trong việc giải các bài tập tương tự. Chúc bạn học tập tốt!
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của hàm số lũy thừa | (x^n)' = nx^(n-1) |
| Đạo hàm của tổng/hiệu | (u ± v)' = u' ± v' |
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của tích | (uv)' = u'v + uv' |
| Đạo hàm của thương | (u/v)' = (u'v - uv')/v^2 |