Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 82 trang 38 Sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ (Oxy) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ (left( { - 4;1} right)) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số. a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn (left[ { - 4;0} right]). b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3
Đề bài
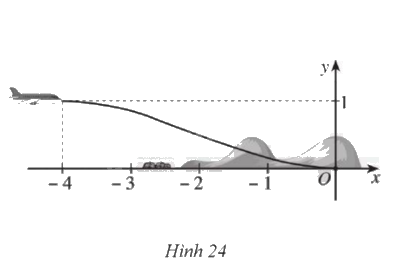
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ \(Oxy\) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ \(\left( { - 4;1} \right)\) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.
a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\).
b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục toạ độ là dặm).
c) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiều dặm?
Phương pháp giải - Xem chi tiết
‒ Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\) dựa vào các điểm trên đồ thị hàm số và các điểm cực trị.
‒ Dựa vào công thức của hàm số để tính khoảng cách giữa máy bay với mặt đất và vị trí hạ cánh theo phương ngang.
Lời giải chi tiết
a) Giả sử đường bay của máy bay có dạng là đồ thị của hàm số \(y = a{x^3} + b{{\rm{x}}^2} + c{\rm{x}} + d\) \(\left( {a \ne 0} \right)\) trên đoạn \(\left[ { - 4;0} \right]\).
\(y' = 3a{x^2} + 2b{\rm{x}} + c\)
Đồ thị hàm số đi qua điểm \(\left( {0;0} \right)\) nên ta có: \(a{.0^3} + b{.0^2} + c.0 + d = 0 \Leftrightarrow d = 0\)
\(x = 0\) là điểm cực tiểu của đồ thị hàm số nên ta có:
\(3a{.0^2} + 2b.0 + c = 0 \Leftrightarrow c = 0\).
Đồ thị hàm số đi qua điểm \(\left( { - 4;1} \right)\) nên ta có:
\(a.{\left( { - 4} \right)^3} + b.{\left( { - 4} \right)^2} + 0.\left( { - 4} \right) + 0 = 1 \Leftrightarrow - 64a + 16b = 1\).
\(x = - 4\) là điểm cực đại của đồ thị hàm số nên ta có:
\(3a.{\left( { - 4} \right)^2} + 2b.\left( { - 4} \right) = 0 \Leftrightarrow 48a - 8b = 0\).
Từ đó ta có \(a = \frac{1}{{32}},b = \frac{3}{{16}},c = 0\).
Vậy hàm số cần tìm là: \(y = \frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2}\).
b) Thay \(x = - 3\), ta được: \(y = \frac{1}{{32}}.{\left( { - 3} \right)^3} + \frac{3}{{16}}.{\left( { - 3} \right)^2} = \frac{{27}}{{32}}\).
Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất \(\frac{{27}}{{32}} = 0,84375\) (dặm).
c) Thay \(y = 0,5\) ta được \(\frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2} = 0,5 \Leftrightarrow x = - 2 - 2\sqrt 3 ,x = - 2 + 2\sqrt 3 ,x = - 2\).
Do \(x \in \left[ { - 4;0} \right]\) nên \(x = - 2\).
Vậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm.
Bài 82 trang 38 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về số phức. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất của số phức để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải toán là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài 82 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 82, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập:
Ví dụ: Tìm phần thực và phần ảo của số phức z = 3 + 2i.
Lời giải:
Phần thực của z là Re(z) = 3.
Phần ảo của z là Im(z) = 2.
Ví dụ: Tính (2 + 3i) + (1 - i).
Lời giải:
(2 + 3i) + (1 - i) = (2 + 1) + (3 - 1)i = 3 + 2i.
Ví dụ: Giải phương trình z2 + (1 + i)z - i = 0.
Lời giải:
Sử dụng công thức nghiệm của phương trình bậc hai, ta có:
Δ = (1 + i)2 - 4(-i) = 1 + 2i - 1 + 4i = 6i.
z1,2 = (-b ± √Δ) / 2a = (-(1 + i) ± √(6i)) / 2
(Việc tính toán căn bậc hai của số phức 6i đòi hỏi kiến thức về dạng lượng giác của số phức và sẽ được trình bày chi tiết hơn trong các bài viết sau).
Ví dụ: Biểu diễn số phức z = -1 + i trên mặt phẳng phức.
Lời giải:
Số phức z = -1 + i được biểu diễn bởi điểm có tọa độ (-1, 1) trên mặt phẳng phức.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 82 trang 38 Sách bài tập Toán 12 - Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!