Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 19 trang 14 Sách bài tập Toán 12 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tìm các khoảng đơn điệu của mỗi hàm số sau: a) \(y = - \frac{1}{3}{x^3} + {x^2} + 3{\rm{x}} - 1\); b) \(y = {x^3} - 3{x^2} + 3{\rm{x}} - 1\); c) \(y = {x^4} + {x^2} - 2\); d) \(y = - {x^4} + 2{{\rm{x}}^2} - 1\); e) \(y = \frac{{2{\rm{x}} - 3}}{{{\rm{x}} - 4}}\); g) \(y = \frac{{{x^2} + x + 2}}{{x + 2}}\).
Đề bài
Tìm các khoảng đơn điệu của mỗi hàm số sau:
a) \(y = - \frac{1}{3}{x^3} + {x^2} + 3{\rm{x}} - 1\); b) \(y = {x^3} - 3{x^2} + 3{\rm{x}} - 1\);
c) \(y = {x^4} + {x^2} - 2\); d) \(y = - {x^4} + 2{{\rm{x}}^2} - 1\);
e) \(y = \frac{{2{\rm{x}} - 3}}{{{\rm{x}} - 4}}\); g) \(y = \frac{{{x^2} + x + 2}}{{x + 2}}\).
Phương pháp giải - Xem chi tiết
Các bước để tìm khoảng đồng biến, nghịch biến của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định của hàm số \(y = f\left( x \right)\).
Bước 2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...,n} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
a) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = - {{\rm{x}}^2} + 2{\rm{x}} + 3\)
\(y' = 0\) khi \(x = - 1\) hoặc \(x = 3\).
Bảng biến thiên của hàm số:
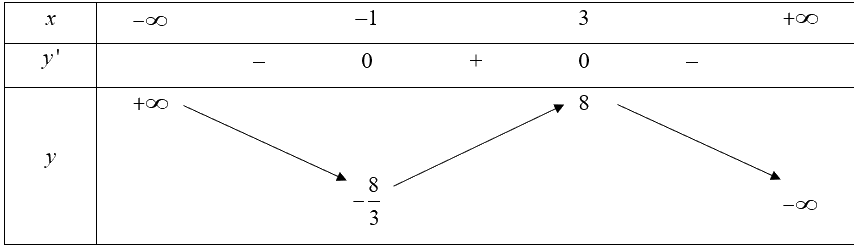
Vậy hàm số đồng biến trên khoảng \(\left( { - 1;3} \right)\); nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\).
b) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = 3{{\rm{x}}^2} - 6{\rm{x}} + 3\)
\(y' = 0\) khi \(x = 1\).
Bảng biến thiên của hàm số: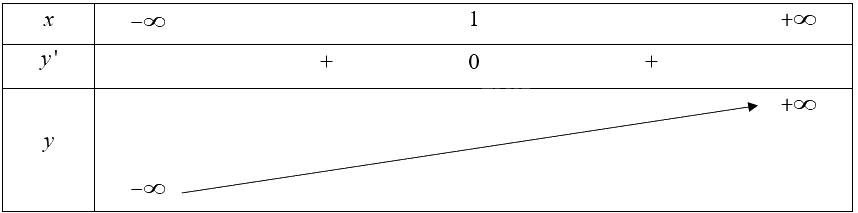
Vậy hàm số đồng biến trên \(\mathbb{R}\).
c) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = 4{{\rm{x}}^3} + 2{\rm{x}}\); \(y' = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
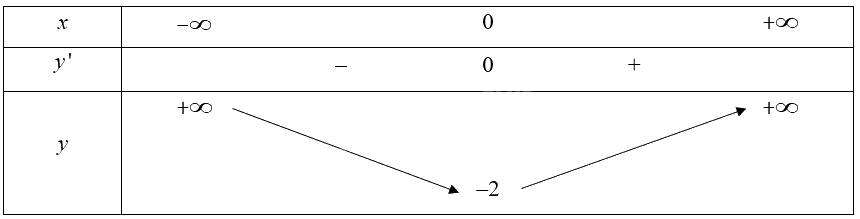
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
d) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = - 4{{\rm{x}}^3} + 4{\rm{x}}\)
\(y' = 0\) khi \(x = 0,x = - 1,x = 1\).
Bảng biến thiên của hàm số:
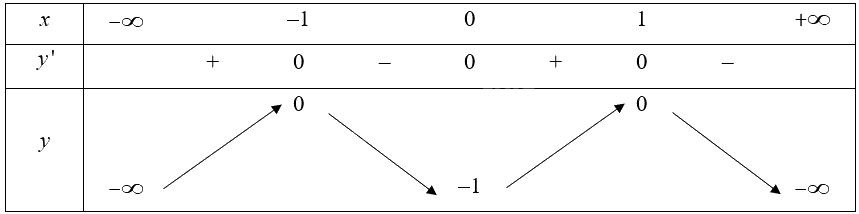
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\); nghịch biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0; + \infty } \right)\).
e) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ 4 \right\}\).
Ta có: \({y^\prime } = - \frac{5}{{{{\left( {x - 4} \right)}^2}}} < 0,\forall x \ne 4\)
Bảng biến thiên của hàm số:
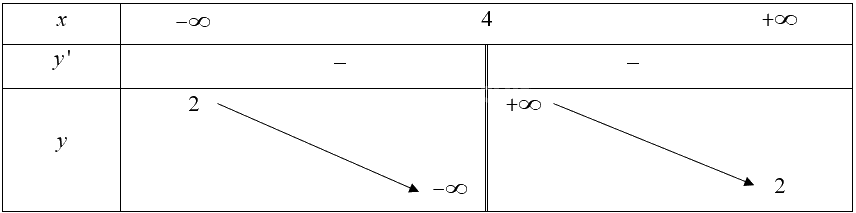
Vậy hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;4} \right)\) và \(\left( {4; + \infty } \right)\).
f) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có:
\(\begin{array}{l}{y^\prime } = \frac{{{{\left( {{x^2} + x + 2} \right)}^\prime }.\left( {x + 2} \right) - \left( {{x^2} + x + 2} \right).{{\left( {x + 2} \right)}^\prime }}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{\left( {2{\rm{x}} + 1} \right)\left( {x + 2} \right) - \left( {{x^2} + x + 2} \right)}}{{{{\left( {x + 2} \right)}^2}}}\\ & = \frac{{{x^2} + 4{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{x\left( {{\rm{x}} + 4} \right)}}{{{{\left( {x + 2} \right)}^2}}}\end{array}\)
\(y' = 0\) khi \(x = 0,x = - 4\).
Bảng biến thiên của hàm số:
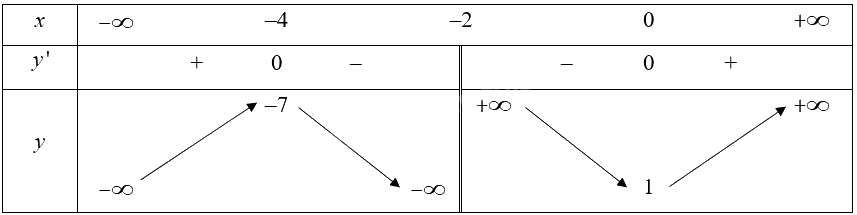
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( {0; + \infty } \right)\); nghịch biến trên mỗi khoảng \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;0} \right)\).
Bài 19 trang 14 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về parabol, đỉnh của parabol, trục đối xứng, giao điểm với trục hoành và trục tung để giải quyết các bài toán thực tế.
Để giải bài 19 trang 14 Sách bài tập Toán 12 - Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 19, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ, nếu bài 19 có 3 câu, sẽ có lời giải cho câu 1, câu 2 và câu 3. Mỗi câu sẽ được trình bày chi tiết, sử dụng các công thức và phương pháp phù hợp.)
Câu 1: Xác định a, b, c của hàm số y = -2x2 + 5x - 3.
Giải:
So sánh hàm số y = -2x2 + 5x - 3 với dạng tổng quát y = ax2 + bx + c, ta có:
Vậy, a = -2, b = 5, c = -3.
Câu 2: Tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Giải:
Hàm số y = x2 - 4x + 3 có a = 1, b = -4, c = 3.
Hoành độ đỉnh của parabol là xI = -b/2a = -(-4)/(2*1) = 2.
Tung độ đỉnh của parabol là yI = (4ac - b2)/4a = (4*1*3 - (-4)2)/(4*1) = (12 - 16)/4 = -1.
Vậy, tọa độ đỉnh của parabol là I(2; -1).
Câu 3: Tìm giao điểm của parabol y = 2x2 + x - 1 với trục hoành.
Giải:
Giao điểm của parabol với trục hoành là nghiệm của phương trình 2x2 + x - 1 = 0.
Giải phương trình 2x2 + x - 1 = 0, ta có:
Δ = b2 - 4ac = 12 - 4*2*(-1) = 1 + 8 = 9.
x1 = (-b + √Δ)/2a = (-1 + √9)/(2*2) = (-1 + 3)/4 = 1/2.
x2 = (-b - √Δ)/2a = (-1 - √9)/(2*2) = (-1 - 3)/4 = -1.
Vậy, giao điểm của parabol với trục hoành là (1/2; 0) và (-1; 0).
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 12 - Cánh Diều và các tài liệu tham khảo khác.
Bài 19 trang 14 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng giúp bạn ôn tập và củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, bạn sẽ giải quyết bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!