Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 15 trang 67 Sách bài tập Toán 12 Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 12 nhé!
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Trong không gian với hệ toạ độ (Oxyz), cho hình hộp (ABCD.A'B'C'D') có (A'left( {1;0;1} right),)(B'left( {2;1;2} right),D'left( {1; - 1;1} right),Cleft( {4;5; - 5} right)). a) Toạ độ của vectơ (overrightarrow {A'D'} ) là (left( {0; - 1;0} right)). b) Gọi toạ độ của điểm (B) là (left( {{x_B};{y_B};{z_B}} right)), ta có toạ độ của vectơ (overrightarrow {BC} ) là (left( {{x_B} - 4;{y_B} - 5;{z_B
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).Trong không gian với hệ toạ độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A'\left( {1;0;1} \right),\)\(B'\left( {2;1;2} \right),D'\left( {1; - 1;1} \right),C\left( {4;5; - 5} \right)\). a) Toạ độ của vectơ \(\overrightarrow {A'D'} \) là \(\left( {0; - 1;0} \right)\). b) Gọi toạ độ của điểm \(B\) là \(\left( {{x_B};{y_B};{z_B}} \right)\), ta có toạ độ của vectơ \(\overrightarrow {BC} \) là \(\left( {{x_B} - 4;{y_B} - 5;{z_B} + 5} \right)\). c) Trong hình hộp \(ABCD.A'B'C'D'\), ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \). d) Toạ độ điểm \(B\) là \(\left( {4;4; - 5} \right)\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
Lời giải chi tiết
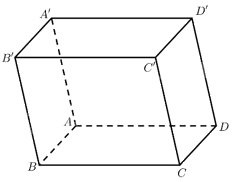
\(\overrightarrow {A'D'} = \left( {1 - 1; - 1 - 0;1 - 1} \right) = \left( {0; - 1;0} \right)\). Vậy a) đúng.
\(\overrightarrow {BC} = \left( {4 - {x_B};5 - {y_B}; - 5 - {z_B}} \right)\). Vậy b) sai.
\(ABCD.A'B'C'D'\) là hình hộp nên \(\overrightarrow {BC} = \overrightarrow {A'D'} \). Vậy c) đúng.
Ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \Leftrightarrow \left\{ \begin{array}{l}4 - {x_B} = 0\\5 - {y_B} = - 1\\ - 5 - {z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 4\\{y_B} = 6\\{z_B} = - 5\end{array} \right.\). Vậy \(B\left( {4;6; - 5} \right)\). Vậy d) sai.
a) Đ
b) S
c) Đ
d) S
Bài 15 trang 67 Sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải toán.
Bài 15 trang 67 Sách bài tập Toán 12 Cánh Diều thường bao gồm các câu hỏi và bài tập liên quan đến:
Để giúp các em học sinh giải bài tập một cách hiệu quả, Giaitoan.edu.vn xin trình bày hướng dẫn giải chi tiết từng bài tập trong bài 15 trang 67 Sách bài tập Toán 12 Cánh Diều:
Đề bài: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Lời giải:
f'(x) = 3x2 - 4x + 5
Đề bài: Tính tích phân xác định ∫01 (x2 + 1) dx.
Lời giải:
∫01 (x2 + 1) dx = [x3/3 + x]01 = (1/3 + 1) - (0 + 0) = 4/3
Để đạt kết quả tốt trong môn Toán 12, các em học sinh cần:
Việc giải bài tập Sách bài tập Toán 12 có vai trò quan trọng trong việc giúp học sinh:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong bài viết này, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán 12. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!