Bài 57 trang 29 Sách bài tập Toán 12 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 57 trang 29 Sách bài tập Toán 12 - Cánh Diều, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S). Cho đồ thị hàm số (y = fleft( x right)) và gọi (S) là diện tích hình phẳng được tô màu như Hình 15. a) (S = intlimits_1^2 {fleft( x right)dx} ). b) (S = intlimits_0^{1,5} {left| {fleft( x right)} right|dx} ). c) (S = intlimits_0^{1,5} {fleft( x right)dx} ). d) (S = intlimits_1^2 {left| {fleft( x right)} right|dx} ).
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
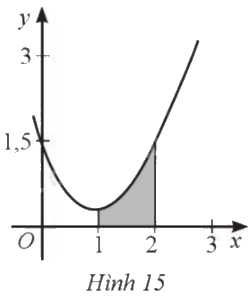
Cho đồ thị hàm số \(y = f\left( x \right)\) và gọi \(S\) là diện tích hình phẳng được tô màu như Hình 15.
a) \(S = \int\limits_1^2 {f\left( x \right)dx} \).
b) \(S = \int\limits_0^{1,5} {\left| {f\left( x \right)} \right|dx} \).
c) \(S = \int\limits_0^{1,5} {f\left( x \right)dx} \).
d) \(S = \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
Hình phẳng đã cho được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 1,x = 2\).
Diện tích hình phẳng được tính theo công thức:
\(S = \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} = \int\limits_1^2 {f\left( x \right)dx} \) (vì \(f\left( x \right) > 0,\forall x \in \left[ {1;2} \right]\)).
Vậy a) đúng, b) sai, c) sai, d) đúng.
a) Đ.
b) S.
c) S.
d) Đ.
Bài 57 trang 29 Sách bài tập Toán 12 - Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường tập trung vào việc tìm đạo hàm, xét tính đơn điệu và cực trị của hàm số, cũng như ứng dụng đạo hàm để giải quyết các bài toán tối ưu hóa.
Thông thường, bài 57 sẽ bao gồm một hoặc nhiều câu hỏi nhỏ, yêu cầu học sinh:
Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài tập 57. Tuy nhiên, dưới đây là một ví dụ minh họa cách giải một bài tập tương tự:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.
Giải:
Để đạt kết quả tốt nhất, học sinh nên:
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 12. Chúng tôi hy vọng sẽ giúp các em học sinh học Toán 12 hiệu quả và đạt kết quả tốt nhất.