Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 12 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 11 trang 96, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm như Bảng 17. a) Tổng số học sinh là 800. b) Số trung bình cộng của mẫu số liệu ghép nhóm đó là: 5,7875. c) Phương sai của mẫu số liệu ghép nhóm đó là: ({s^2} approx 3,85). d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: (s = sqrt {3,85} approx 1,962).
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Một trung tâm ngoại ngữ thực hiện kiểm tra đầu vào của 80 học sinh đăng kí học, kết quả kiểm tra được cho bởi bảng tần số ghép nhóm như Bảng 17.
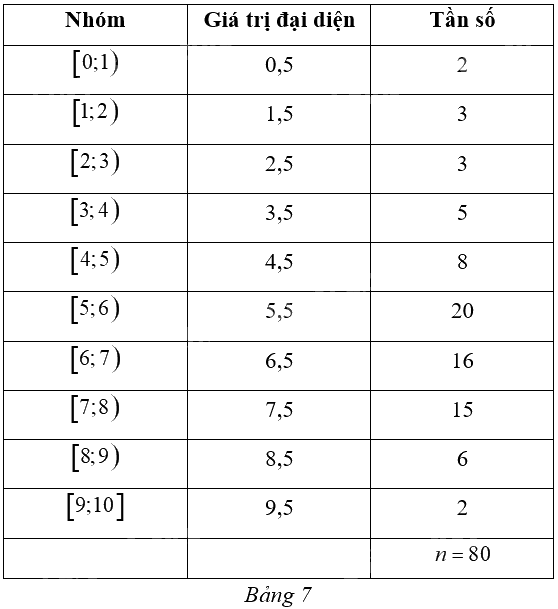
a) Tổng số học sinh là 800.
b) Số trung bình cộng của mẫu số liệu ghép nhóm đó là: 5,7875.
c) Phương sai của mẫu số liệu ghép nhóm đó là: \({s^2} \approx 3,85\).
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: \(s = \sqrt {3,85} \approx 1,962\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính số trung bình cộng của mẫu số liệu ghép nhóm: \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1,...,k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(s = \sqrt {{s^2}} \).
Lời giải chi tiết
Tổng số học sinh là: \(n = 80\). Vậy a) sai.
Số trung bình cộng của mẫu số liệu ghép nhóm ở Bảng 17 là:
\(\overline x = \frac{{2.0,5 + 3.1,5 + 3.2,5 + 5.3,5 + 8.4,5 + 20.5,5 + 16.6,5 + 15.7,5 + 6.8,5 + 2.9,5}}{{80}} = \frac{{463}}{{80}} = 5,7875\)
Vậy b) đúng.
Phương sai của mẫu số liệu ghép nhóm đó là:
\(\begin{array}{l}{s^2} = \frac{1}{{80}}\left[ {2.{{\left( {0,5 - 5,7875} \right)}^2} + 3.{{\left( {1,5 - 5,7875} \right)}^2} + 3.{{\left( {2,5 - 5,7875} \right)}^2} + 5.{{\left( {3,5 - 5,7875} \right)}^2} + } \right.\\ + 8.{\left( {4,5 - 5,7875} \right)^2} + 20.{\left( {5,5 - 5,7875} \right)^2} + 16.{\left( {6,5 - 5,7875} \right)^2} + 15.{\left( {7,5 - 5,7875} \right)^2} + \\\left. { + 6.{{\left( {8,5 - 5,7875} \right)}^2} + 2.{{\left( {9,5 - 5,7875} \right)}^2}} \right] = \frac{{24671}}{{6400}} \approx 3,85\end{array}\)
Vậy c) đúng.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {3,85} \approx 1,962\). Vậy d) đúng.
a) S.
b) Đ.
c) Đ.
d) Đ.
Bài 11 trang 96 sách bài tập toán 12 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán thực tế.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của bài 11 trang 96 sách bài tập toán 12 - Cánh diều:
(Giả sử đề bài là: Cho hàm số f(x) = x^3 - 3x^2 + 2. Tìm đạo hàm f'(x) và giải phương trình f'(x) = 0.)
Để giải bài toán này, chúng ta cần:
Bước 1: Tính đạo hàm f'(x)
Áp dụng quy tắc đạo hàm của hàm đa thức, ta có:
f'(x) = d/dx (x^3 - 3x^2 + 2) = 3x^2 - 6x
Bước 2: Giải phương trình f'(x) = 0
Ta có phương trình:
3x^2 - 6x = 0
Rút gọn phương trình:
3x(x - 2) = 0
Suy ra:
x = 0 hoặc x = 2
Vậy, phương trình f'(x) = 0 có hai nghiệm là x = 0 và x = 2.
Kết luận: Bài 11 trang 96 sách bài tập toán 12 - Cánh diều đã được giải quyết thành công. Chúng ta đã tìm được đạo hàm f'(x) và các nghiệm của phương trình f'(x) = 0.
Mở rộng: Bài tập này là một ví dụ điển hình về việc ứng dụng đạo hàm để tìm các điểm cực trị của hàm số. Trong quá trình học tập, bạn nên luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng giải toán.
Ngoài bài 11 trang 96, sách bài tập toán 12 - Cánh diều còn có nhiều bài tập tương tự về đạo hàm. Dưới đây là một số dạng bài tập bạn có thể tham khảo:
Để học tốt về đạo hàm, bạn nên:
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài 11 trang 96 sách bài tập toán 12 - Cánh diều. Chúc bạn học tập tốt!